Skis

The stiffer your skis, the faster you can ski, but it also becomes more difficult to navigate turns. During landings, less of the force is absorbed through bending, resulting in harder impacts on your knees. The stiffness of skis can be described using linear springs. Linear springs are mechanical components that produce a force proportional to the deflection. The stiffness k is measured in Newtons per meter (N/m). When springs are connected in parallel, think of two skis next to each other, the effective stiffness corresponds to the sum of the individual springs’ stiffness.

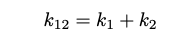
In a telemark landing, the skis are positioned partly behind each other. If they were placed completely in line, they would be connected in series. When springs are arranged in series, the inverse stiffness is equal to the sum of the inverses of the individual springs’ stiffnesses.

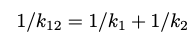
Springs that are connected in series are represented by placing them between square brackets [k1, k2]. Springs that are connected in parallel are represented between round brackets (k1, k2).

BONUS:

A network of springs can consist of combinations of springs connected in parallel and in series. For example, this is represented as “[10, (30, 40)]”.

The following complex network of springs:

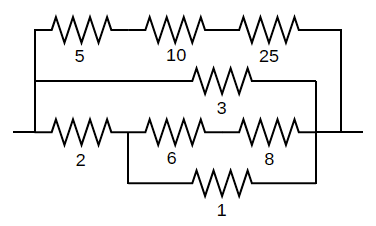
is represented by the string: “([5, 10, 25], (3, [2, ( [6, 8], 1)]))”

Assignment

• Write a function parallel that combines the stiffness of two or more springs that are connected in parallel. The input for the function is a tuple of two or more decimal numbers. The output is a decimal number with a precision of one decimal place.
• Write a function serie that combines the stiffness of two or more springs that are connected in series. The input for the function is a list of two or more decimal numbers. The output is a decimal number with a precision of one decimal place.
• Write a functionstiffness that reads a string variable and calls the functions parallel and serie to calculate the stiffness of a combination of two or more springs connected either in parallel or in series.
• Write a function message that reads a decimal number, like the output of the stiffness function, and converts it into a message: “The stiffness of the network is x N/m”, where x is the given decimal number.
• Tip: Create the easier functions first.
• BONUS: adjust the function stiffness so that it reads a string variable and returns the stiffness for a combination of springs connected in series and/or parallel.

Example

>>> k1k2 = (1.0, 2.0)
>>> parallel(k1k2)
3.0
>>> k3k4 = [7.0, 8.0]
>>> serie(k3k4)
3.7
>>> stiffness("(5, 5)")
10.0
>>> stiffness("[5, 5]")
2.5
>>> stiffness("(20,30)")
50.0
>>> stiffness("[10,20]")
6.7
>>> message(22.0)
The stiffness of the network is 22.0 N/m

Example bonus

>>> stiffness("[10, (30, 40)]")
8.8