The dirty truth about mathematics parties

In "Catalan numbers and RNA secondary structures¹" we talked about counting the number of ways for an even number of people to shake hands at a party without crossing hands. However, in the real world, parties only contain an even number of people about 30% of the time, and mathematicians aren't social butterflies. So we should instead count the total number of ways for some of the people at the party to shake hands without crossing.

In the biological world, people are perhaps more social, but not every nucleotide in a strand of RNA winds up base pairing with another nucleotide during RNA folding. As a result, we want to loosen this assumption and count the total number of different secondary structures of an RNA strand whose base pairs don't overlap (i.e., we still forbid pseudoknots in the strand).

Assignment

Similarly to our definition of the Catalan numbers, the $$n$$-th Motzkin number $$M_n$$ counts the number of ways to form a (not necessarily perfect) non-crossing matching in the complete graph $$K_n$$ containing $$n$$ nodes. For example, the figure below demonstrates that $$M_5 = 21$$. Note in this figure that technically, the "trivial" matching that contains no edges at all is considered to be a matching, because it satisfies the defining condition that no two edges are incident to the same node.

The 21 distinct ways to form a noncrossing matching on 5 labeled nodes.

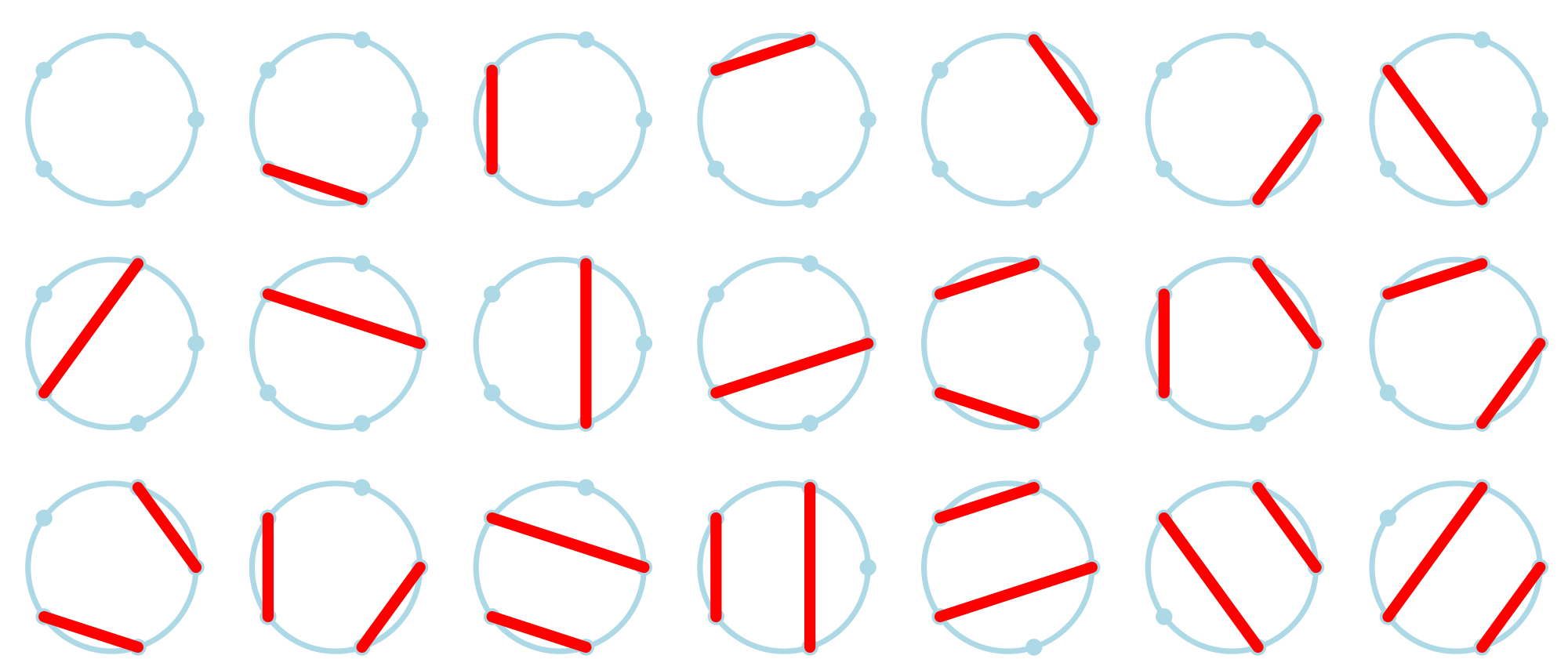
How should we compute the Motzkin numbers? As with Catalan numbers, we will take $$M_0 = M_1 = 1$$. To calculate $$M_n$$ in general, assume that the nodes of $$K_n$$ are labeled around the outside of a circle with the integers between 1 and $$n$$, and consider node 1, which may or may not be involved in a matching. If node 1 is not involved in a matching, then there are $$M_{n - 1}$$ ways of matching the remaining $$n - 1$$ nodes. If node 1 is involved in a matching, then say it is matched to node $$k$$: this leaves $$k - 2$$ nodes on one side of edge $$\{1, k\}$$ and $$n - k$$ nodes on the other side. As with the Catalan numbers, no edge can connect the two sides, which gives us $$M_{k - 2}\cdot M_{n - k}$$ ways of matching the remaining edges. Allowing $$k$$ to vary between $$2$$ and $$n$$ yields the following recurrence relation for the Motzkin numbers: \[ M_n = M_{n - 1} + \sum_{k=2}^n{M_{k - 2}\cdot M_{n - k}} \]

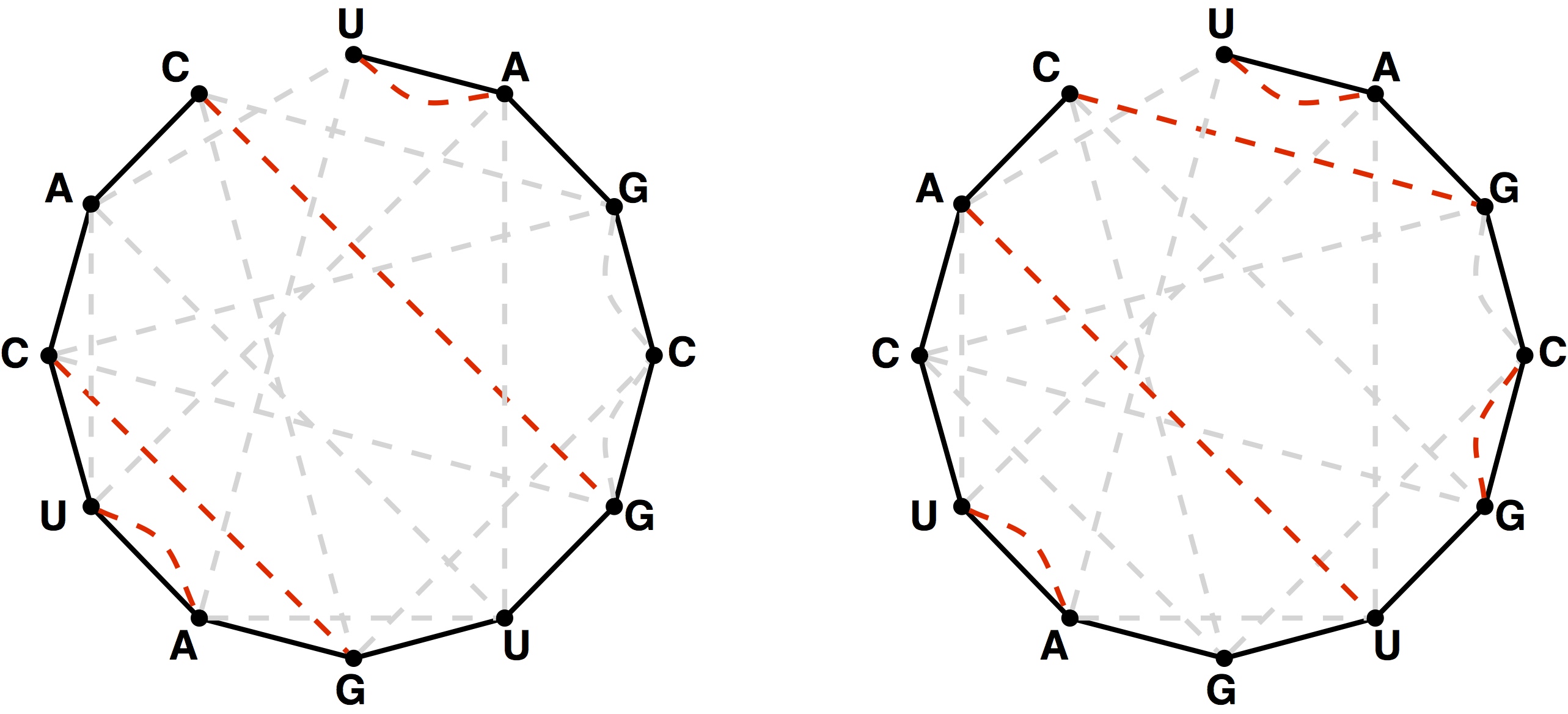
To count all possible secondary structures of a given RNA string that do not contain pseudoknots, we need to modify the Motzkin recurrence so that it counts only matchings of basepair edges in the bonding graph corresponding to the RNA string.

Two possible noncrossing matchings of basepair edges in the bonding graph corresponding to RNA string UAGCGUGAUCAC.

Your task:

Write a function motzkinNumber that takes an integer $$n \in \mathbb{N}$$ and returns the Motzkin number $$M_n$$.
Write a function noncrossingMatchings that takes an RNA strings $$s$$. The function must return the total number of non-crossing matchings of basepair edges in the bonding graph of $$s$$ modulo 1,000,000.

Example

In the following interactive session, we assume the FASTA file data.fna² to be located in the current directory.

        >>> motzkinNumber(0)
1
>>> motzkinNumber(1)
1
>>> motzkinNumber(2)
2
>>> motzkinNumber(3)
4
>>> motzkinNumber(4)
9
>>> motzkinNumber(5)
21
>>> motzkinNumber(21)
142547559

>>> noncrossingMatchings('AUAU')
7
>>> from Bio import SeqIO
>>> noncrossingMatchings(*SeqIO.parse('data.fna', 'fasta'))
872195