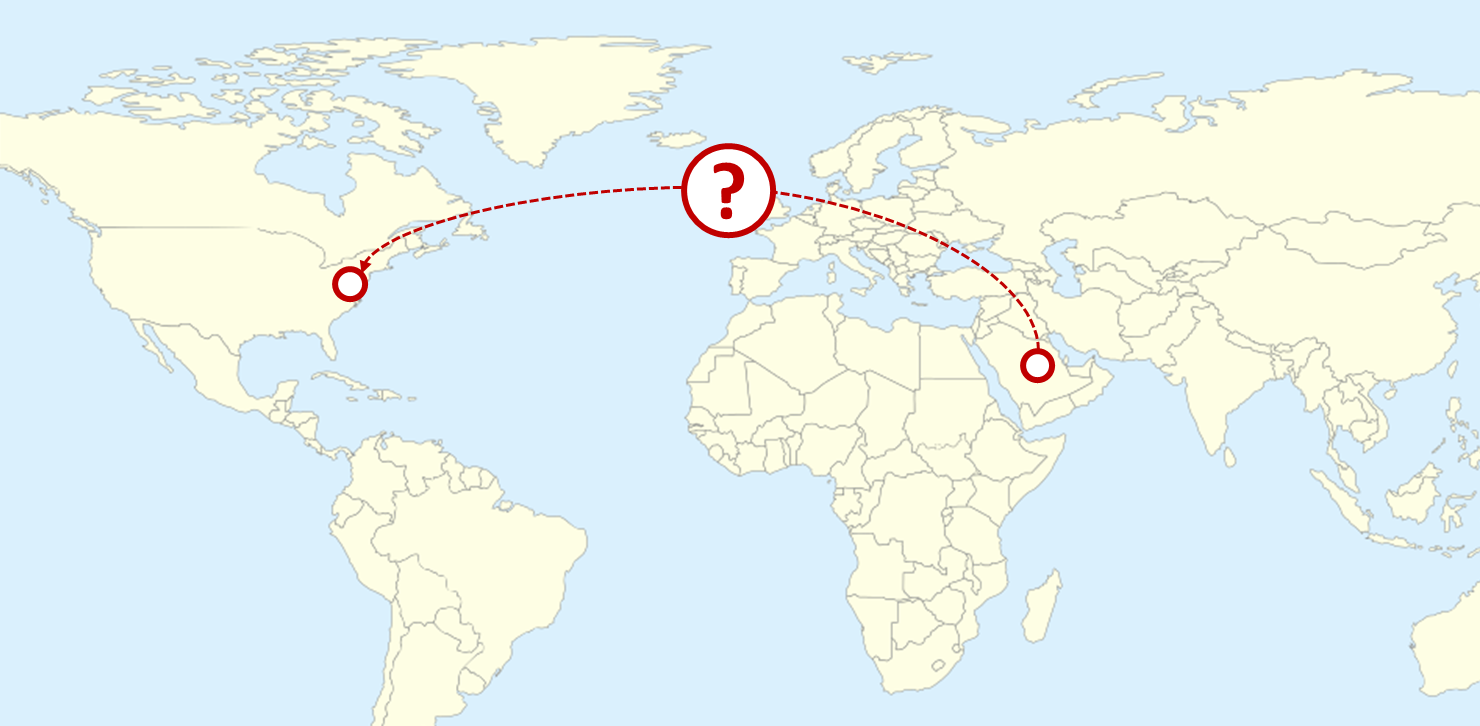
If Equatorial Guinea is halfway between Angola and Mauritius, Norway is halfway between El Salvador and Iran, Fiji is halfway between Spain and Gabon, and Ireland is halfway between South Korea and French Guiana, which country is halfway between Saudi Arabia and the United States of America?

Which country is halfway between Saudi Arabia and the United States of America?

Assignment

If you try to determine the "halfway" relationships on a globe, you'll quickly notice that they are not correct. Instead we use the international standard ISO 3166-1¹ that defines for each country a unique two-letter code (alpha-2), a unique three-letter code (alpha-3) and a unique three-digit code (numeric-3). This standard is recorded in the text file iso_3166-1.txt²:

Country;Alpha-2 code;Alpha-3 code;Numeric code;Latitude (average);Longitude (average)
Afghanistan;AF;AFG;004;33;65
Albania;AL;ALB;008;41;20
Algeria;DZ;DZA;012;28;3
American Samoa;AS;ASM;016;-14.3333;-170
Andorra;AD;AND;020;42.5;1.6
Angola;AO;AGO;024;-12.5;18.5
Anguilla;AI;AIA;660;18.25;-63.1667
Antarctica;AQ;ATA;010;-90;0
Antigua and Barbuda;AG;ATG;028;17.05;-61.8
…

The first line of the file contains a header. Every other line describes a country using six information fields separated by semicolons (;): i) unique name, ii) unique two-letter code (alpha-2), iii) unique three-letter code (alpha-3), iv) unique three-digit code (numeric-3), v) (average) latitude and vi) (average) longitude. The information fields themselves do not contain semicolons.

For each country we use the three-letter code consisting of three uppercase letters. To determine the midpoint of two codes, we first define how the midpoint of two letters is determined. We use two alternative definitions for this. The symmetric midpoint of two letters has a position in the alphabet that is exactly midway between the positions of the two letters, regardless of the order of those two positions. For example, the letter J is the symmetric midpoint of the letters F and N that are eight positions apart in the alphabet, and it is also the symmetric midpoint of the letters N and F.

The symmetric midpoint of two letters has a position in the alphabet that is exactly midway between the positions of the two letters, regardless of the order of those two positions.

We can also put the letters of the alphabet clockwise around a circle, with the letter Z followed by the letter A. In this case it takes 8 steps to go clockwise around the circle from the letter F to the letter N, so the letter J is the asymmetric midpoint of the letters F and N, because it is $$\frac{8}{2} = 4$$ steps clockwise around the circle away from the letter F. But it takes 18 steps to go clockwise around the circle from the letter N to the letter F, so the letter W is the asymmetric midpoint of the letters N and F, because it is $$\frac{18}{2} = 9$$ steps clockwise around the circle away from the letter N.

The asymmetric midpoint of two letters has a position in a circular clockwise alphabet that is clockwise exactly midway between the position of the first letter and the position of the second letter.

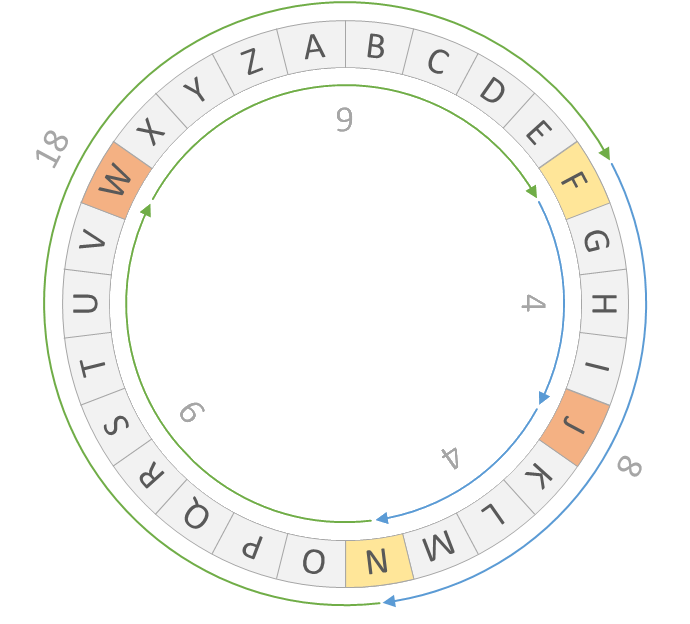
An alternative way to determine the asymmetric midpoint is to repeat the entire alphabet twice. In this double alphabet, we determine the position where the first letter occurs first, and then the position where the second letter occurs first from the position of the first letter.

The midpoint of two three-letter codes is then a string (str) of three uppercase letters, where the first letter is the midpoint of the first letters of both codes, the second letter is the midpoint of the second letters of both codes and the third letter is the midpoint of the third letter of both codes. Your task:

Write a function read_standard that takes the location (str) of a text file specifying a standard with unique country codes, formatted as the file iso_3166_1.txt³. The function must return a dictionary (dict) that maps the name (str) of each country in the file onto a tuple (tuple) containing three strings (str) with the unique country codes: i) two-letter code (alpha-2), ii) three-letter code (alpha-3), and iii) three-digit code (numeric-3). We call this the country code dictionary for the given standard.
Write a function reverse that takes a country code dictionary $$\mathcal{C}$$. The function must return a new dictionary (dict) that maps all three-letter codes (str; alpha-3) from $$\mathcal{C}$$ onto the name (str) of the corresponding country.
Write a function midletter that takes two uppercase letters (str). If the number of steps in the alphabet between these two letters is odd, an AssertionError must be raised with the message no midpoint. Otherwise the function must return the midpoint of the two given letters. The function also has an optional parameter asymmetric that may take a Boolean value (bool; default value: False). The value of this parameter determines whether the symmetric (False) or the asymmetric (True) midpoint must be returned.
Write a function midcode that takes two three-letter codes (str). If the number of steps in the alphabet between two corresponding letters of these codes is odd, an AssertionError must be raised with the message no midpoint. Otherwise the function must return the midpoint of the two given codes. The function also has an optional parameter asymmetric that may take a Boolean value (bool; default value: False). The value of this parameter determines whether the symmetric (False) or the asymmetric (True) midpoint must be returned.
Write a function halfway that takes three arguments: the names (str) of two countries and a country code dictionary $$\mathcal{C}$$. The function must return the name (str) of the country whose three-letter code is the midpoint of the three-letter codes of the two given countries, based on the countries and their country codes defined in $$\mathcal{C}$$. If this country can not be determined, an AssertionError must be raised with the message no midpoint. The function also has an optional parameter asymmetric that may take a Boolean value (bool; default value: False). The value of this parameter determines whether the symmetric (False) or the asymmetric (True) midpoint must be used.

Example

In the following interactive session we assume the text file iso_3166_1.txt⁴ to be located in the current directory.

        >>> country2codes = read_standard('iso_3166_1.txt5')
>>> country2codes['Angola']
('AO', 'AGO', '024')
>>> country2codes['Mauritius']
('MU', 'MUS', '480')
>>> country2codes['Equatorial Guinea']
('GQ', 'GNQ', '226')

>>> code2country = reverse(country2codes)
>>> code2country['AGO']
'Angola'
>>> code2country['MUS']
'Mauritius'
>>> code2country['GNQ']
'Equatorial Guinea'

>>> midletter('F', 'N')
'J'
>>> midletter('N', 'F')
'J'
>>> midletter('F', 'N', asymmetric=True)
'J'
>>> midletter('N', 'F', asymmetric=True)
'W'
>>> midletter('A', 'D')
Traceback (most recent call last):
AssertionError: no midpoint

>>> midcode('AGO', 'MUS')
'GNQ'
>>> midcode('ISL', 'CYP')
'FVN'
>>> midcode('ISL', 'CYP', asymmetric=True)
'SVN'
>>> midcode('KHM', 'VNM')
Traceback (most recent call last):
AssertionError: no midpoint

>>> halfway('Angola', 'Mauritius', country2codes)
'Equatorial Guinea'
>>> halfway('Iceland', "Cyprus", country2codes)
Traceback (most recent call last):
AssertionError: no midpoint
>>> halfway('Iceland', "Cyprus", country2codes, asymmetric=True)
'Slovenia'