Andrea's only timepiece is a large grandfather clock that is fixed to the wall. One day she forgets to wind it and it stops. A few days later, she travels across town to have dinner with a friend whose own clock is always correct. When she returns home, she makes a simple calculation and sets her own clock accurately.

How does she manage to do this without knowing the travel time between her house and her friend's?

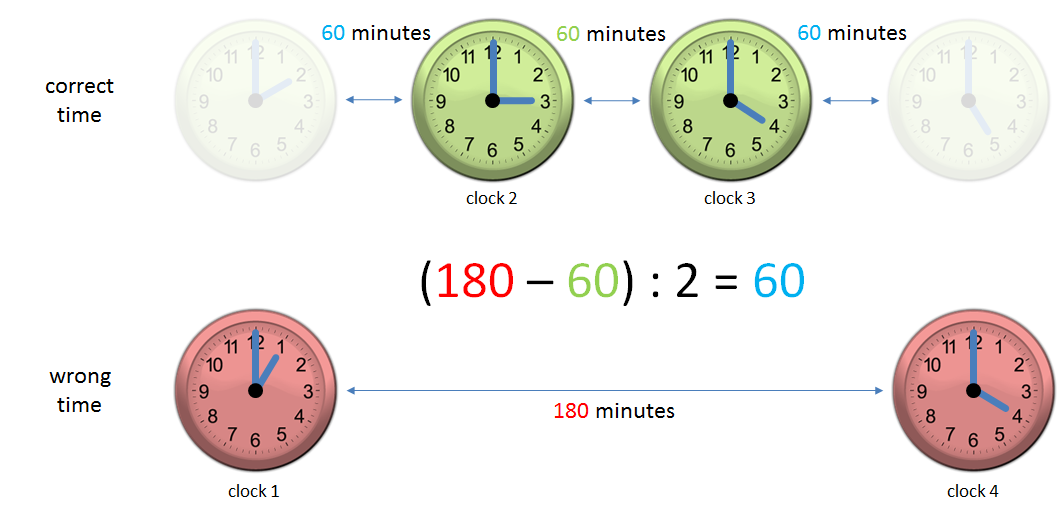
With some creative thinking the solution is not that hard to execute. Before she leaves the house, Andrea winds her own clock and sets it to an arbitrary time. Then she notes the correct time at her friend's house both when she arrives and when she leaves. When she returns home she consults her own clock to see how much time the whole trip has taken, subtracts the period she spent at her friend's house, and divides the result by two to learn the travel time in each direction. By adding this interval to the time she noted as she left her friend's house, she can infer the current time and set her own clock.

Input

Eight integers, each on a separate line. Each pair of consecutive integers $$h$$ ($$0 \leq h < 24$$) and $$m$$ ($$0 \leq m < 60$$) corresponds to the timestamp $$h\text{:}m$$ on a 24-hour clock. The four timestamps consecutively indicate the time at which Andrea

• leaves her own house

• arrives at her friend's house

• leaves her friend's house

• returns to her own house

Output

Two lines containing the integers $$h$$ ($$0 \leq h < 24$$) and $$m$$ ($$0 \leq m < 60$$) that correspond to the correct time $$h\text{:}m$$ on a 24-hour clock when Andrea returns to her own house. You may assume that the total time Andrea is away from home is at most 24 hours.

Example

Input:

13
0
15
0
16
0
16
0

Output:

17
0