The Maya settled in Central-America at the beginning of our era. In many ways, they were by far the most developed and fascinating civilization of their time. Wheels and draft animals were unknown to them, yet they mastered the art of weaving, architecture and pottery like no other. But truly breathtaking were their achievements in mathematics and astronomy. While Europe was dragging itself through the Dark Ages, the Maya calculated the solar year at 365,242 days (by modern reckoning 365,242198 days) and the lunar cycle at 29,5302 days (by modern reckoning 29,53059 days). Such astonishingly accurate calculations would hardly have been without the powerful Mayan number system.
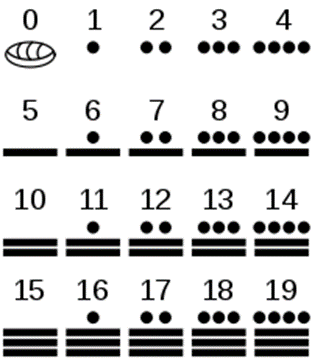
Mayan priests and astronomers used a number system with base 20 in which the digits (0-19) are represented by three symbols: zero (shape of a shell), one (a dot) and five (a horizontal bar). For example, nineteen (19) is written as four dots next to each other horizontally, above three horizontal bars stacked on top of each other. The concepts of 'digit' and 'zero' were quite unusual for the time, and still completely unknown in Europe.
For Mayan numbers consisting of multiple Mayan digits — that is, numbers with a value larger than 19 — the Mayan digits are written vertically on top of each other. The digit with the highest numerical value is at the top. For example, the number thirty-three (33) is written as a dot (upper Mayan digit) above three dots on top of two horizontal bars (lower Mayan digit). The first dot represents "one twenty" or $$1 \times 20$$, to which three dots and two horizontal bars (i.e. 13) are added. This way, we get $$(1 \times 20) + 13 = 33$$.
| unit | 33 | 389 | 4645 | 66876 |
|---|---|---|---|---|
| 7200 |
|
|||
| 360 |
|
|
|
|
| 20 |
|
|
|
|
| 1 |
|
|
|
|
Strangely enough, in the Mayan number system, the digit in the third position (counted from the bottom) does not have value of $$20 \times 20 = 400$$, but $$18 \times 20 = 360$$. Presumably because 360 is roughly equal to the number of days in a calendar year. All Mayan digits above the third position (counted from the bottom) again have a normal numerical value according to the base 20 system, so for the fourth digit $$360 \times 20 = 7200$$, for the fifth digit $$7200 \times 20 = 144000$$, and so on. For example, the table above shows that \[ 12 \times 360 + 16 \times 20 + 5 = 4645 \] and that \[ 9 \times 7200 + 5 \times 360 + 13 \times 20 + 16 = 66876 \]
Assignment
The string representation of a Mayan number is a string (str) listing the Mayan digits of the Mayan number from top to bottom and separated by a space. The Mayan digit with value zero is written as the letter S. The other Mayan digits are written as zero or more dots (.; value 1) followed by zero or more dashes (-; value 5). This way, the Mayan number with decimal value 66876 is represented as the string ....- - ...-- .---.
Define a class Maya that can be used to represent Mayan numbers in Python. Make sure that Mayan numbers can be created from their decimal value $$d$$ (int; $$0 \leq d$$), from their string representation (str) or from another Mayan number (Maya). If a Mayan number (Maya) is created from an invalid object, an AssertionError must be raised with message invalid Mayan number.
The conversion of a Mayan number (Maya) to a string (str) — obtained with the built-in functions str and repr — always contains the string representation (str) of the Mayan number (you can derive the difference in the result that both built-in functions return from the example below) and the conversion to an integer (int) — obtained with the built-in function int — returns the decimal value (int) of the Mayan number.
Make sure that the binary operations for addition (+), subtraction (-), multiplication (*), integer division (//), modulo (%), and exponentiation (**) each return a new Mayan number (Maya) if both operands are Mayan numbers (Maya) or if one of the two operands is a Mayan number (Maya) and the other is an integer (int). The result of those operations must have the same decimal value as the result these operations produce for two integer operands with the same decimal value. If an operation does not produce a valid Mayan number, an AssertionError must be raised with message invalid Mayan number.
Example
>>> a = Maya('..')
>>> int(a)
2
>>> b = Maya(33)
>>> str(b)
'. ...--'
>>> c = a + b
>>> c
Maya('. ---')
>>> print(c)
. ---
>>> int(c)
35
>>> a - b
Traceback (most recent call last):
AssertionError: invalid Mayan number
>>> b - a
Maya('. .--')
>>> a * b
Maya('... .-')
>>> int(a * b)
66
>>> b // a
Maya('.---')
>>> b % a
Maya('.')
>>> int(b ** a)
1089
>>> Maya('... .- . ..') + 89343
Maya('--- ....-- .... -')
>>> int(74837 - Maya('.... --- ...- ....--'))
40463
>>> Maya('....- ..-- ....-') * 2478
Maya('... S S --- ..--- ..')
>>> Maya(34783 // Maya('. .- ..-'))
Maya('... .--')
>>> Maya('..- -- ..--') % 89
Maya('... ..')
>>> Maya('..-- -') ** 7
Maya('....-- ..- ....- ..- ..- - .--- . ..-- .--- ...-- ..-- -')
>>> Maya('xxx')
Traceback (most recent call last):
AssertionError: invalid Mayan number
>>> Maya('SS ..--')
Traceback (most recent call last):
AssertionError: invalid Mayan number
>>> Maya('.....--')
Traceback (most recent call last):
AssertionError: invalid Mayan number
>>> Maya('..-- .- ...--- ...---')
Traceback (most recent call last):
AssertionError: invalid Mayan number