During maths you’ve learned how to determine the distance between 2 points \(\mathsf{(x_1, y_1)}\) and \(\mathsf{(x_2,y_2)}\). This formula boils down to an application of the pythagorean theorem.

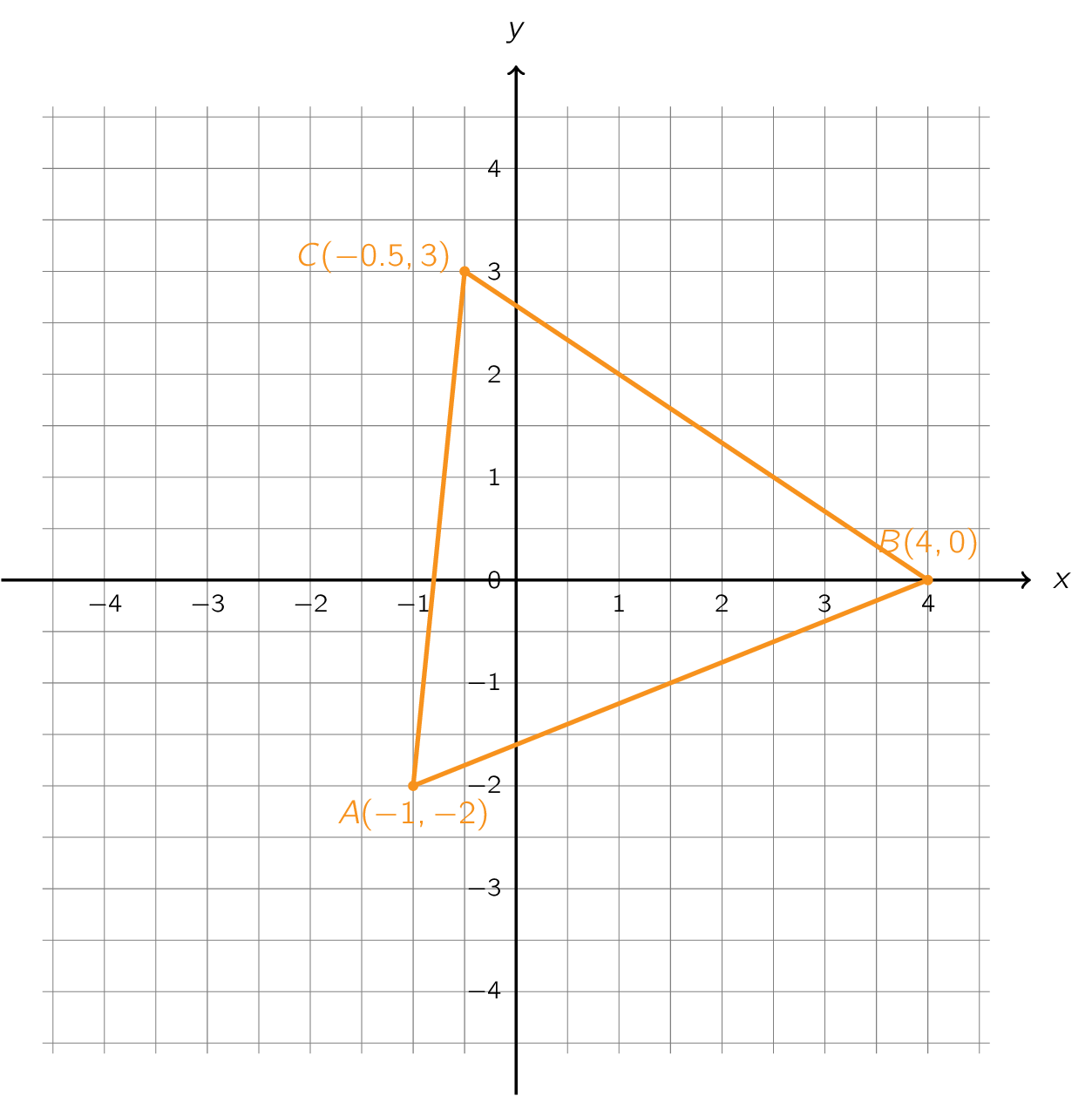
Assignment

Create a function afstand(x1, y1, x2, y2) that calculates the distance between \(\mathsf{(x_1, y_1)}\) and \(\mathsf{(x_2,y_2)}\). Round this distance to a single decimal point.

In the program below we’re asking the coordinates of three vertices A, B and C. Use the function afstand() to determine whether the coordinates form an equilateral, an isosceles or a scalene triangle.

Examples

For the coordinates A(0,0), B(4, 0) and C(2,5) we expect:

Driehoek ABC is gelijkbenig. # Triangle ABC is an isosceles triangle.

because

>>> afstand(0, 0, 4, 0)
4.0
>>> afstand(0, 0, 2, 5)
5.4
>>> afstand(4, 0, 2, 5)
5.4

For the coordinates A(0,0), B(4, 0) and C(2,3.46) we expect:

Driehoek ABC is gelijkzijdig. # Triangle ABC is an equilateral triangle.

because

>>> afstand(0, 0, 4, 0)
4.0
>>> afstand(0, 0, 2, 3.46)
4.0
>>> afstand(4, 0, 2, 3.46)
4.0

Hint

Don’t forget to import the math library…