In general, instead of arbitrarily choosing \(\lambda = 4\), it would be better to
use cross-validation to choose the tuning parameter \(\lambda\). We can do this using
the built-in cross-validation function, cv.glmnet(). By default, the function
performs ten-fold cross-validation, though this can be changed using the
argument folds. Note that we set a random seed first so our results will be
reproducible, since the choice of the cross-validation folds is random.
> set.seed(1)
> cv.out <- cv.glmnet(x[train,], y[train], alpha = 0)
> plot(cv.out)
> bestlam <- cv.out$lambda.min
> bestlam
[1] 326.0828
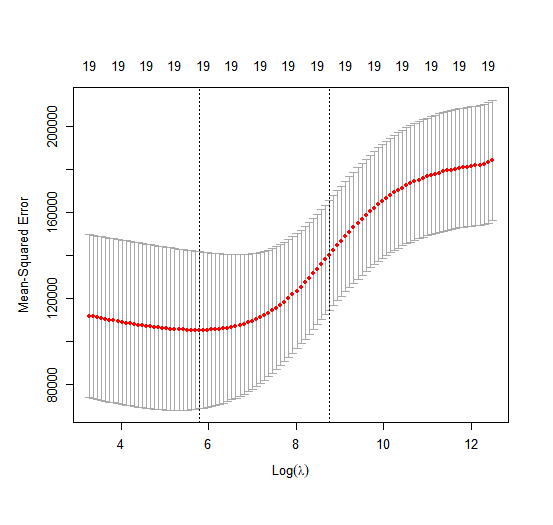
Therefore, we see that the value of \(\lambda\) that results in the smallest cross-validation error is 326. What is the test \(MSE\) associated with this value of \(\lambda\)?
> ridge.pred <- predict(ridge.mod, s = bestlam, newx = x[test,])
> mean((ridge.pred - y.test)^2)
[1] 139856.6
This represents a further improvement over the test \(MSE\) that we got using \(\lambda\) = 4. Finally, we refit our ridge regression model on the full data set, using the value of \(\lambda\) chosen by cross-validation, and examine the coefficient estimates.
> out <- glmnet(x, y, alpha = 0)
> predict(out, type = "coefficients", s = bestlam)[1:20,]
(Intercept) AtBat Hits HmRun
15.44383135 0.07715547 0.85911581 0.60103107
Runs RBI Walks Years
1.06369007 0.87936105 1.62444616 1.35254780
CAtBat CHits CHmRun CRuns
0.01134999 0.05746654 0.40680157 0.11456224
CRBI CWalks LeagueN DivisionW
0.12116504 0.05299202 22.09143189 -79.04032637
PutOuts Assists Errors NewLeagueN
0.16619903 0.02941950 -1.36092945 9.12487767
As expected, none of the coefficients are zero, ridge regression does not perform variable selection!
Using the Boston dataset, try determining the lambda that minimizes the \(MSE\) (store it in bestlam) using the cross-validation approach (store the cross-validation output in cv.out).
With the acquired \(\lambda\), determine the ridge regression predictions (store them in ridge.pred) and calculate the \(MSE\) (store it in ridge.mse).
Assume that:
- The
MASSandglmnetlibraries have been loaded - The
Bostondataset has been loaded and attached - The seed is set on 1.
- The variables
x,ycreated in exercise Ridge Regression 1 are already loaded - The variables
train,test,y.testandridge.modcreated in exercise Ridge Regression 4 are already loaded