Er bestaan twee gangbare manieren om elk punt van een vlak voor te stellen door een paar van coördinaten: cartesische coördinaten en poolcoördinaten. Het eerste coördinatensysteem is het bekendste. Hierin wordt elk punt voorgesteld door een \(x\)- en een \(y\)-coördinaat. In het tweede coördinatensysteem wordt elk punt voorgesteld door een straal \(r\) (de afstand tot de oorsprong) en een hoek \(\theta\) (de hoek tussen de verbinding met de oorsprong en de positieve -as). Natuurlijk bestaat er een verband tussen deze twee coördinatensystemen. Als een punt de coördinaten \((x,y)\) en \((r,\theta)\) heeft, dan gelden de volgende verbanden:

\[\begin{aligned} \left\{ \begin{array}{rcl} x&=&r\cos(\theta) \\ y&=&r\sin(\theta) \end{array} \right. \end{aligned}\]

en

\[\begin{aligned} \left\{ \begin{array}{rcl} r&=&\sqrt{x^2+y^2} \\ \theta&=&\arctan(\frac{y}{x}) \end{array} \right. \end{aligned}\]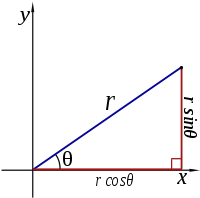

Om deze oefening op te lossen heb je functies uit de module math nodig. Zoek de beschikbare functies op in de API¹.

Je kan een lijst met functies ook in Python:

import math
help(math) 

Bekijk het verschil tussen de functies atan en atan2. Je kan dit opzoeken in module math².

Invoer

De invoer bestaat uit twee reële getallen, elk op een afzonderlijke regel, die respectievelijk de \(x\)- en \(y\)-coördinaat van een gegeven punt in het cartesisch coördinatensysteem voorstellen.

Uitvoer

De uitvoer bestaat uit twee reële getallen, elk op een afzonderlijke regel, die respectievelijk de straal \(r\) en de hoek \(\theta\) van het gegeven punt in poolcoördinaten uitdrukken.

Voorbeeld 1

Invoer

1
0

Uitvoer

1.0
0.0

Voorbeeld 2

Invoer

0
3

Uitvoer

3.0
1.5707963267948966