History

Darts is an age-old game that originates among soldiers who started competitions as a pastime between battles. They threw short arrows at the bottom of wine barrels and later at discs made of the trunks of trees. Scores were added onto the discs. Out of necessity, the sport was played inside during the winter months, which forced the soldiers to replace the arrows with darts and led to a new set of rules for practicing the indoor sport. As the game continued to develop, the richer layers of population gained an interest in darts. It is written that Hendrik VIII's second wife Anne Boleyn gave him a richly decorated Biscayan darts set.

Dartboard

The current game board comes from London. The board consists of a round fiber plate of 18 millimetres thick, on which sisal fiber bristles are glued and pressed under large pressure. The whole is framed by a metal band. The board is provided with a section division using different colours. After that, a metal web is fixed on top of the plate, provided with the same division. The function of this web is to make sure it is always clear in which section the dart landed. On the outer border, a metal ring is placed on which numbers are fixed according to the section division. This ring can be unlinked from the rest of the board, making it possible to shift the numbers with regard to the plate.

The idea is that the section (bed) 20 is in the middle on top. This section is usually the most thrown on. This is why the bottom plate of this section is likely to break first. Every dart that is thrown affects the fibers of the board. The glue layer prevents the board from falling apart, but after a while, an accumulation of fibers will be visible under the form of lumps. To prevent this, the board should be turned around as much as possible, so that 20 is always on top of another section. Do note that 20 should always be on top of a black section. Modern sisal fiber boards shouldn't be made wet (unlike what is often thought).

A dartboard.

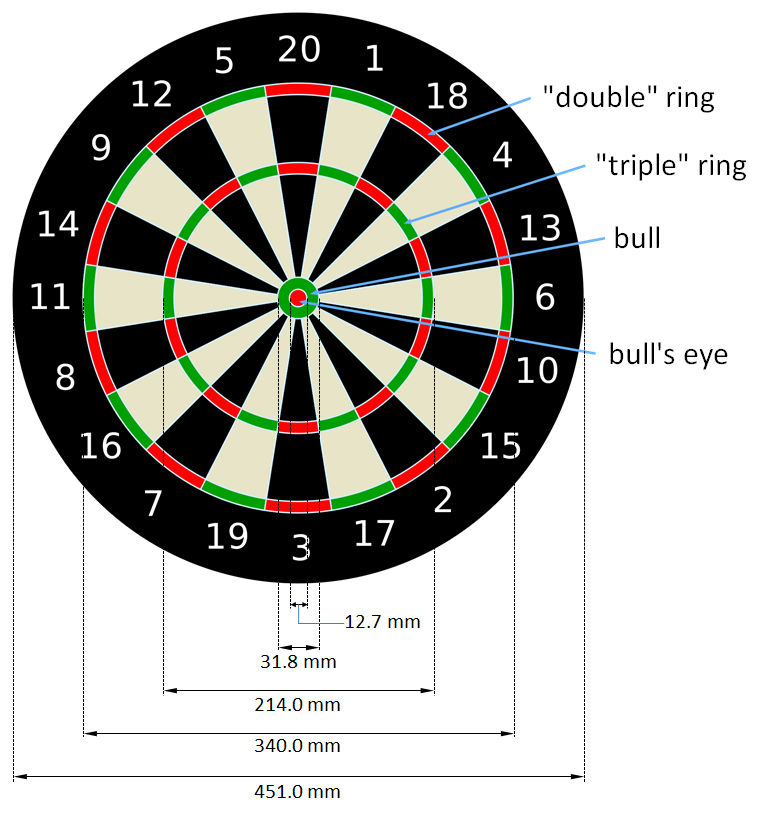
The measurements of a dartboard are indicated in the picture above. The double ring and triple ring are always 9.6 mm wide.

Scoring

The dartboard is divided in rings and sections. The numbers at the rim indicate the amount of points you receive for throwing a dart in that particular section. The sections are subdivided in a number of smaller partitions.

in the middle is the double bull or bull's eye (red), 50 points
around the double bull is the single bull (green), 25 points
around that a wide ring, the bed (black and white), for which the amount of points that is indicated on the rim of the board is granted
around that a smaller ring, the triple (or treble) ring (red and green); this yields a triple score of the bed
around that is another bed
around that is the double ring (red en green) yields a double score of the bed

If you throw a dart in the outer black rim (where the numbers are) or next to the board, you don't get any points. A bouncer, which is a dart that bounces back from the board, doesn't get a score. You also won't receive any points if one of your darts falls out of the board before you were able to take your darts out (please note, officially this isn't called a bouncer). If a player throws in one of his formerly thrown darts (a 'Robin Hood'), the last dart doesn't receive a score.

Assignment

We consider a Cartesian co-ordinate scale¹ with its origin in the centre of the bull's eye of a dartboard. A player throws a dart to the board that lands on co-ordinates $$(x, y)$$, the co-ordinates are expressed in millimetres. Determine the score that is obtained by this dart. Work as follows:

Write a function polar to which two real numbers $$x$$ and $$y$$ must be given. These numbers represent the position $$(x, y)$$ of a point $$P$$ in the Cartesian co-ordinates scale. The function must print a tuple $$(r, \theta)$$ of real numbers, that expresses the position of a point $$P$$ in polar co-ordinates², where the pole $$O$$ coincides with the centre of the bull's eye, and the pole axis coincides with the $$X$$ axis. The co-ordinate $$r$$ of the point $$P$$ is the distance $$OP$$. The co-ordinate $$\theta$$ indicates the oriented angle between the positive $$X$$ axis and the half straight line of O through P. This angle is expressed in radians, and $$-\pi < \theta \leq \pi$$ must apply.

$$(r, \theta)$$ is a set of pole co-ordinates of the point $$P$$.

The connection between the Cartesian co-ordinates $$(x, y)$$ and the pole co-ordinates $$(r, \theta)$$ is than given by \[\begin{cases} r = & \sqrt{x^2+y^2} \\ \\ \theta = & \arctan\left(\frac{y}{x}\right) \end{cases}\]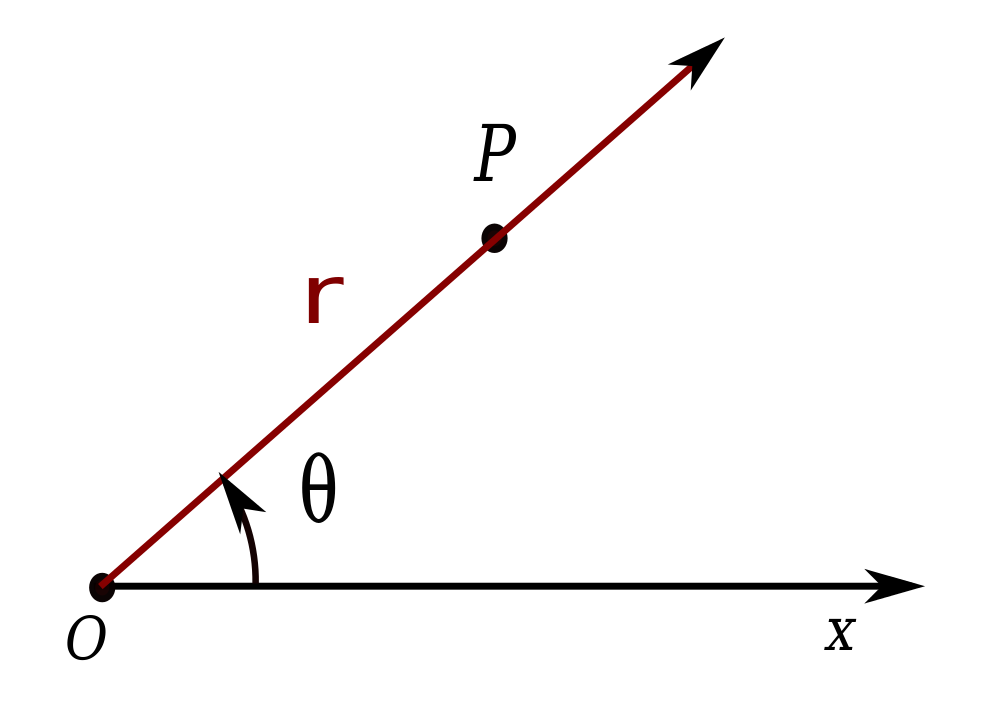
Use the function polar to write a function darts, to which two integers $$x$$ and $$y$$ must be given. These numbers represent the position $$(x, y)$$ of a point $$P$$ in the Cartesian co-ordinates scale, and are expressed in millimetres. As a third, optional argument scores, a sequence (or a list or tuple) of integers can be given to this function. The amount of numbers in the sequence determines the number of sectors in which the dartboard is divided. The numbers indicate the scoring if the sectors are run through clockwise, starting with the section that contains the points on the positive $$Y$$ axis. This last sector is always situated symmetrically with regard to the positive $$Y$$ axis. If no explicit score was given to the function, use the score 1, 2, …, 20. The function must print the score that is obtained if a dart that is thrown at the board and lands on the position $$(x, y)$$ in the Cartesian co-ordinate scale with its origin in the centre of the bull's eye.

From angle to sector

One of the difficulties of this exercise is how to determine the sector on the board in which the dart is thrown. The sketch given below illustrates how an angle in polar coordinates ($$\theta$$; the green angle) can be converted into an angle ($$\beta$$; the red angle) that can be used to determine the corresponding sector.

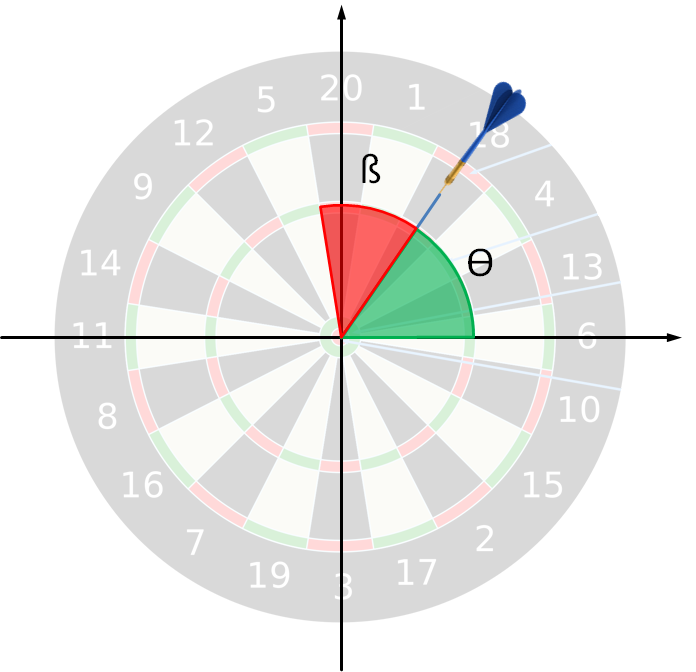
Using a little bit of trigonometry, it is easy to see that \[ \beta + \theta = \frac{\pi}{2} + \frac{\pi}{s}\,, \] where $$s$$ represents the number of sectors. In other words, \[ \beta = \frac{\pi}{2} + \frac{\pi}{s} - \theta\,. \] Once $$\beta$$ has been computed and you know that each sector covers an angle of $$\frac{2\pi}{s}$$, you can convert the angle $$\beta$$ into the index of the sector. The first sector (the one on top of the $$Y$$-axis) has index 0, the one to the right of it has index 1, and so on in a clockwise manner.

Example

>>> polar(137, 0)
(137.0, 0.0)
>>> polar(104.5, 0)
(104.5, 0.0)
>>> polar(0, 200)
(200.0, 1.5707963267948966)
>>> polar(0, 166.3)
(166.3, 1.5707963267948966)
>>> polar(-30.0, 22.0)
(37.20215047547655, 2.5088438185876103)

>>> darts(137, 0)
6
>>> darts(104.5, 0)
18
>>> darts(0, 200)
0
>>> darts(0, 166.3)
2
>>> darts(-30.0, 22.0)
18

>>> points = [20, 1, 18, 4, 13, 6, 10, 15, 2, 17, 3, 19, 7, 16, 8, 11, 14, 9, 12, 5]
>>> darts(137, 0, scores=points)
6
>>> darts(104.5, 0, scores=points)
18
>>> darts(0, 200, scores=points)
0
>>> darts(0, 166.3, scores=points)
40
>>> darts(-30.0, 22.0, scores=points)
9