In 2012 The Royal Society wrote a report entitled Shut down or restart?1 that was hammering on the way 21st century education in the UK treated computer science skills. British politics immediately understood the huge shortcomings in this area, and took the radical decision to make computer science an integral part of curricula for primary and secondary education starting from September 2015. As a result, all British school children now learn to program computers starting at the age of 5.
In the slipstream of this educational reform, a whole bunch of teaching material was developed to help children discover the wonderful world of computing. For example, the initiative CS unplugged2 — computer science without a computer — develops puzzles to stimulate problem solving skills using paper and pencil only, or chalk on the playground.

This assignment is inspired by one of the CS unplugged activities that uses a magic trick to show how computers can detect when data has been corrupted, and how to correct it3. When data is stored on a disk or transmitted from one computer to another, we usually assume it doesn't get changed in the process. But sometimes things go wrong and the data is changed accidentally. During this activity, children learn how they can detect if errors have corrupted the data, and how they can be corrected. The activity only requires a complete deck of 52 playing cards. The activity goes as follows:
-
Choose a child to lay out the playing cards in a rectangular $$r \times c$$ grid with $$r$$ rows and $$c$$ columns. The grid must show a random mixture of cards facing up and down.
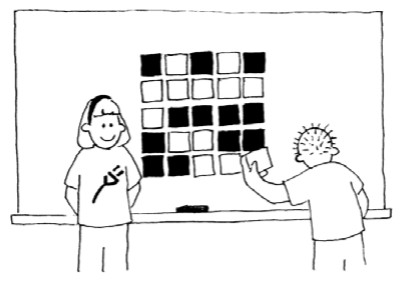
Step 1: Arrange the playing cards in a rectangular grid, with a random mixture of cards facing up or down. -
Casually add another row and column, "just to make it a bit harder". These extra cards are the key to the trick. You must choose the extra cards to ensure that there is an even number of cards facing up in each row and in each column.
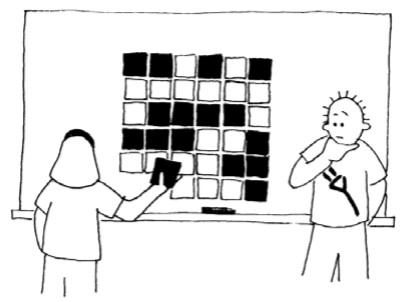
Step 2: Extend the grid with an extra row and an extra column, such that each row and column have an even number of cards facing up. -
Get another child to flip over a single card while you cover your eyes. The row and column containing the flipped card will now have an odd number of cards facing up, which allows you to easily identify the flipped card.
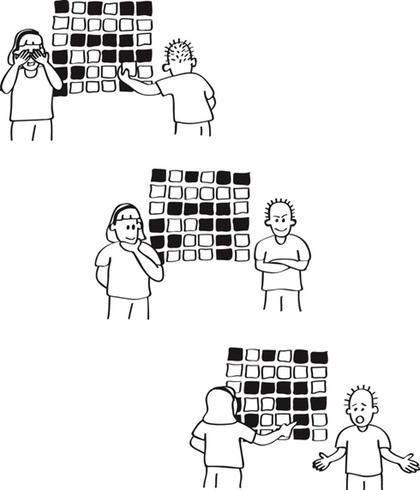
Step 3: Flip a random card, whose row and column now contain an odd number of cards facing up. -
Ask all children to guess how the trick is done. Does the trick still work if you would flip two or more cards in the grid?
Opgave
A complete deck of playing cards contains 52 cards that are grouped into four suits of 13 cards each: 13 spades (♠), 13 hearts (♥), 13 clubs (♣) en 13 diamonds (♦). Each suit has cards of the following ranks: 2 to 10, a jack, a queen, a king and an ace. In this assignment we will represent a playing card as a two-character string. The first character represents the rank of the playing card with possible values the digits 2 up to and including 9 and the capitals X (ten), J (jack), Q (queen), K (king) and A (ace). The second character represents the suit of the playing card: S (spades), H (hearts), C (clubs) or D (diamonds). As such, the playing card AS represents the ace of spades.
In this assignment we ask to implement four functions that can be used to arrange playing cards from a complete deck of cards in a rectangular grid, to extend a grid of cards with an extra row and column, and to select a random card in a grid of cards. We represent a rectangular grid of cards as a list of rows of playing cards listed from top to bottom, with each row of playing cards itself being represented as a list of playing cards listed from left to right. All playing cards in a grid are randomly drawn from a complete set of playing cards, such that each playing card may occur at most once in the grid. Your task:
-
Write a function draw that returns a random playing card from a complete deck of playing cards, with each card having the same probability of being drawn from the deck. The function has an optional parameter drawn that takes a container (a list, a tuple or a set) of playing cards, representing the playing cards that have already been drawn. If a container of playing cards is passed to the parameter drawn, the function draw may never return a playing card from this container.
-
Write a function arrange that has two optional parameters rows and cols (default value for both parameters is 5). The function must return a rectangular grid of playing cards with the given number of rows and columns. The cards that are arranged in the grid must be randomly drawn from a complete set of playing cards. As a result, each playing card may occur at most once in the grid. The grid should have at least one row and at least one column, and may contain no more than 52 playing cards. If this would not be the case, the function must raise an AssertionError with the message invalid grid.
-
Write a function extend that takes a rectangular grid of playing cards. The function must extend the given grid of playing cards by adding an extra column to the right and adding an extra row to the bottom. The cards used to extend the grid must come from the same complete deck of cards that was used to arrange to given grid. In case the given grid cannot be extended with an extra row and an extra column, because there are not enough cards in a complete deck, the function must raise an AssertionError with the message invalid grid.
-
Write a function select that takes a rectangular grid of playing cards. The function must return the position of a random card in the grid. Positions of cards arranged in a rectangular grid are represented as a tuple of two positive integers that respectively indicate the row and column index of the cards in the grid. The rows of the grid are indexed top to bottom, and the columns left to right, starting from zero. Make sure that each card in the grid has equal probability of being selected.
Example
>>> draw()
'6S'
>>> draw(['6H', '3C', '3D', '8C', 'AD', '9D', '7D', 'QC'])
'4D'
>>> draw(drawn=('3S', '8H', '8C', '2H', 'AC'))
'XH'
>>> draw({'4C', 'AH', 'JS', '7S', '9H', '2H', 'QC', '2S', '3H', '7C'})
'9S'
>>> arrange(rows=3, cols=4)
[['5D', '4D', '4C', '9S'], ['2D', '6C', '4S', 'AD'], ['QH', 'QS', '2S', '3D']]
>>> arrange(rows=7, cols=8)
Traceback (most recent call last):
AssertionError: invalid grid
>>> grid = [['QH', '9S', '3C'], ['5D', '8C', '2H']]
>>> extend(grid)
>>> grid
[['QH', '9S', '3C', 'JH'], ['5D', '8C', '2H', '9H'], ['XD', 'XC', '4C', '9C']]
>>> grid = [['RA', 'K6', 'RV', 'H7'], ['R6', 'KX', 'KX', 'KV'], ['R8', 'R4', 'R7', 'K3']]
>>> select(grid)
(1, 3)