Intermezzo probabiliteitstheorie

Discrete toevallig veranderlijken

Stel dat we een discrete random variabele meten \(X\). Alle mogelijke waarden voor \(X\) worden de steekproefruimte \(\Omega\) genoemd.

Voor Gender is de steekproefruimte \(\Omega=(0,1)\) met 0 (vrouw) or 1 (man).
Voor het werpen van een dobbelsteen is de steekproefruimte \(\Omega=(1,2,3,4,5,6)\).

Een event \(A\) is een subset van de steekproefruimte

Een even getal werpen met een dobbelsteen: \(A=(2,4,6)\).
Kan ook een specifieke waarde zijn \(A=(1)\).

Event ruimte \(\mathcal{A}\) is de klasse van alle mogelijke events die kunnen optreden bij een bepaald experiment.

Twee events (\(A_1\) en \(A_2\)) zijn multueel exclusief als ze niet samen op kunnen treden.

v.b. event van de oneven getallen \(A_1=(1,3,5)\) en het event om \(A_2=(6)\) te gooien.
Dus \(A_1 \bigcap A_2=\emptyset\).

Probabiliteit \(Pr(A)\) is een function \(Pr: A \rightarrow [0,1]\) die voldoet aan

\(Pr(A) \geq 0\) en \(Pr(A) \leq 1\) voor elke \(A \in \mathcal{A}\).
\(Pr(\Omega)=1\).
Voor multueel exclusieve events \(A_1, A_2, \ldots A_k\) geldt dat \(Pr(A_1 \cup A_2 \ldots \cup A_k)= Pr(A_1) + \ldots + Pr(A_k)\).

Dobbelsteen voorbeeld

oneven number \(A=(1,3,5)\): is de unie van 3 multueel exclusieve events \(A_1=1\), \(A_2=3\) en \(A_3=5\) zodat \(Pr(A)=Pr(1)+Pr(3)+Pr(5)=1/6+1/6+1/6=0.5\)
\(\Omega=(1,2,3,4,5,6)\): \(Pr(\Omega)=1\)

Als we twee subjecten (j en k) onafhankelijk trekken van de populatie dan is de gezamelijke probabiliteit \(P(X_j,X_k)= P(X_j)P(X_j)\)

Distributie of verdeling

De distributie of de verdeling van een discrete toevallig veranderlijke \(X\) beschrijft de kans op elke mogelijke waarde van de steekproefruimte.

Voorbeeld: Gender is een binaire variabele (0: vrouw, 1: man) en binaire variabelen volgen een Bernoulli verdeling. 50.8% van de subjecten in de Amerikaanse populatie zijn vrouw en 49.2% is man.

Laat \(\pi\) de probabiliteit zijn op een man \(\pi=0.492\).

\[X\sim \left \{ \begin{array}{lcl} P(X=0) &=& 1-\pi\\ P(X=1) &=& \pi \end{array} \right .\]

    tibble(X=c(0,1),prob=c(0.508,0.492)) %>%
      ggplot(aes(x=X,xend=X,y=0,yend=prob)) +
      geom_segment() +
      ylab("Probability")

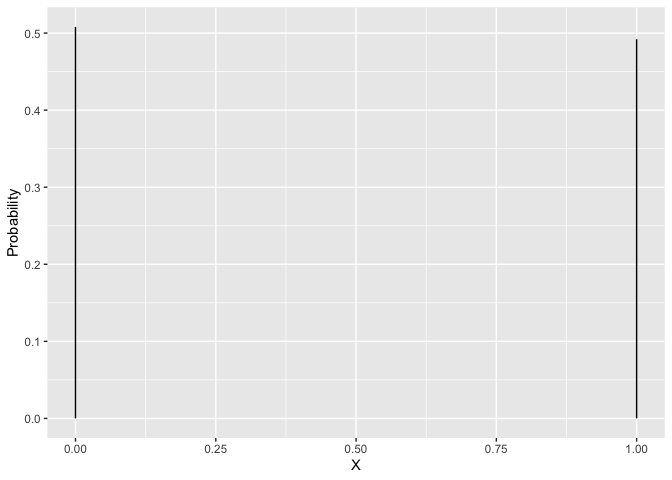
Toevallig veranderlijke \(X\) volgt een Bernoulli verdeling \(B(\pi)\) met parameter \(\pi=0.492\),

\[B(\pi)= \pi^x(1-\pi)^{(1-x)}\]

Cumulative distributie functie

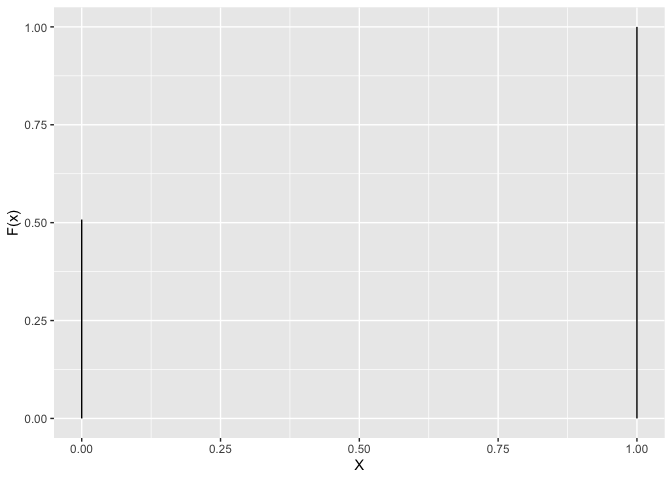
De cumulative distributie functie F(x) geeft de probabiliteit weer om een random variable X te observeren waarvoor geldt dat \(X\leq x\):

\[F(x) = \sum\limits_{\forall X\leq x} P(x)\]

Gender voorbeeld \(F(0)=1-\pi\) and \(F(1)= P(X=0) + P(X=1)=1\)

    tibble(X=c(0,1),cumprob=c(0.508,1)) %>%
      ggplot(aes(x=X,xend=X,y=0,yend=cumprob)) +
      geom_segment() +
      ylab("F(x)")

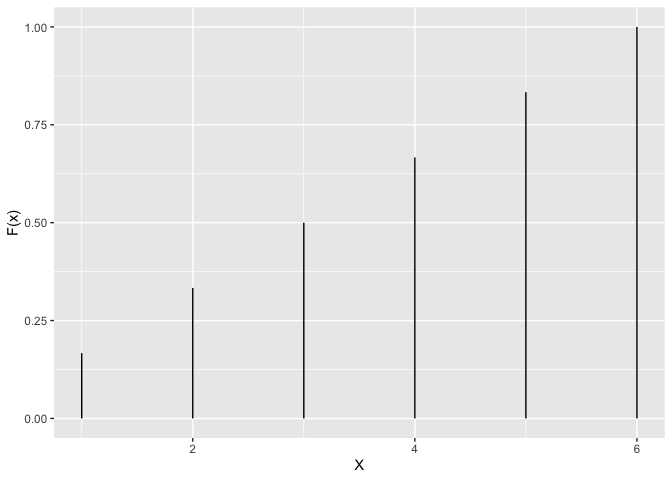
Dobbelsteen voorbeeld:

    tibble(X=1:6,cumprob=cumsum(rep(1/6,6))) %>%
      ggplot(aes(x=X,xend=X,y=rep(0,6),yend=cumprob)) +
      geom_segment() +
      ylab("F(x)")