Genome assembly is the computational process in which the actual sequence of nucleotides making up an organism's genome is determined. Researchers are presently unable to read the nucleotides of an entire chromosome one at a time. Instead, they rely on high-technological chemical methods to determine the order of bases along short strands of DNA (usually less than 1000 bp). These short strands are called reads.
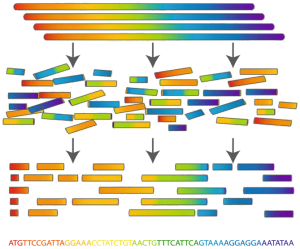
To sequence a genome, researchers chemically "blow up" multiple copies of a genome (typically taken from multiple cells of the same organism) into reads and then determine the nature of the reads. To reassemble the genome, they must use overlaps in reads to determine which read pairs are adjacent in the genome. For example, if the short reads GACCTACA and ACCTACAA are produced, then we might surmise from the fact that they overlap that they both belong to a substring GACCTACAA. An efficient algorithm for assembly that can handle all possible wrinkles and complications arising from practical concerns (such as errors in reads) still does not exist, so that research in genome assembly remains a highly competitive field.
In this assignment we solve a simplified version of the genome assembly problem, where all reads have a fixed length $$k$$ ($$k$$-mers), all $$k$$-mers in the original genome occur just once and there are no read errors.
Assignment
We start by breaking up a given word in all its $$n - k + 1$$ overlapping substrings of length $$k$$. These are called the $$k$$-mers of the given word. Then we randomly shuffle the list of $$k$$-mers. The problem you're now faced with is to reconstruct the original word. For example, consider the following list of four substrings of length 3 (given here in alphabetic order):
ANA ANA BAN NAN
These are the four 3-mers of the word BANANA. Your task:
-
Write a function kmers that takes two arguments: i) a string containing $$n$$ letters (where $$3 \leq n \leq 100.000$$) $$$$ and ii) an integer $$k \in \mathbb{N}$$ (where $$2 \leq k \leq 15$$ and $$k \leq n$$). The function must return a list containing the $$n - k + 1$$ overlapping substrings of length $$k$$ of the given string string. There is no imposed order in which these $$k$$-mers must be listed.
-
Write a function assemble that takes a list of $$k$$-mers. Each of these $$k$$-mers must be a string containing $$k \in \mathbb{N}$$ letters (where $$2 \leq k \leq 15$$). The function must return a string of length $$n \in \mathbb{N}$$ whose $$n - k + 1$$ overlapping substrings of length $$k$$ correspond to the given list of $$k$$-mers, irrespective of the order in which the $$k$$-mers are listed. In case it is impossible to compose such a string, the function must raise an AssertionError with the message invalid k-mers.
Although this is a simplified version of the true genome assembly problem, this problem in itself is quite challenging in providing an efficient solution. Your challenge is not only to come up with a program that can find a least one solution, but also to try to make that program as fast as possible. You may find some inspiration for solving this problem in the paper of Compeau et al. (2011). In practice, genome assemblies are made from millions of reads with lengths between 40 and 10.000 base pairs (dependent on the sequence technology used), that need to be composed into genomes with lengths in the orders of millions or billions of base pairs.
Example
>>> kmers('banana', 2)
['ba', 'an', 'na', 'an', 'na']
>>> kmers('cucumber', 2)
['cu', 'uc', 'cu', 'um', 'mb', 'be', 'er']
>>> kmers('elderberry', 3)
['eld', 'lde', 'der', 'erb', 'rbe', 'ber', 'err', 'rry']
>>> kmers('pineapple', 3)
['pin', 'ine', 'nea', 'eap', 'app', 'ppl', 'ple']
>>> kmers('mississippi', 3)
['mis', 'iss', 'ssi', 'sis', 'iss', 'ssi', 'sip', 'ipp', 'ppi']
>>> kmers('alfalfa', 3)
['alf', 'lfa', 'fal', 'alf', 'lfa']
>>> assemble(['an', 'an', 'ba', 'na', 'na'])
'banana'
>>> assemble(['be', 'cu', 'cu', 'er', 'mb', 'uc', 'um'])
'cucumber'
>>> assemble(['ber', 'der', 'eld', 'erb', 'err', 'lde', 'rbe', 'rry'])
'elderberry'
>>> assemble(['app', 'eap', 'ine', 'nea', 'pin', 'ple', 'ppl'])
'pineapple'
>>> assemble(['ipp', 'iss', 'iss', 'mis', 'ppi', 'sip', 'sis', 'ssi', 'ssi'])
'mississippi'
>>> assemble(['alf', 'alf', 'fal', 'lfa', 'lfa'])
'alfalfa'
Challenge
Now that you have implemented an algorithm that reconstructs words from a shuffled list of all its $$k$$-mers, try to see how fast the algorithm works. The file words8.txt contains a list of 70.000+ English words of at least 8 characters, each word on a separate line. Modify your program such that it takes each word in this list, splits it into all its $$k$$-mers (pick a fixed $$k$$; the problem becomes more difficult with smaller $$k$$) and then try to reconstruct the original word from its k-mers. Analyze the behavior of your "assembly" program:
- how fast can your program process and reconstruct all words in the given file?
- how many words are reconstructed correctly? how do you define "correct" in your evaluation?
- in what situations does the algorithm fail?
- what if some $$k$$-mers are missing, does the algorithm still works? what if some $$k$$-mers are sampled more than once? (sampling with replacement)
- what if some $$k$$-mers contain errors, how does the algorithm cope with that?
Resources
-
Baker M (2012). De novo genome assembly: what every biologist should know. Nature Methods 9, 333-337.
-
Compeau PEC, Philip EC, Pevzner PA, Tesler G (2011). How to apply de Bruijn graphs to genome assembly. Nature Biotechnology 29(11), 987-991.
-
Miller JR, Koren S, Sutton G (2010). Assembly algorithms for next-generation sequencing data. Genomics 95(6), 315-327.
-
Schatz MC, Delcher AL, Salzberg SL (2010). Assembly of large genomes using second-generation sequencing. Genome Research 20, 1165-1173.