In the world's oceans, you cannot go further from any land than Point Nemo before you start coming back. Point Nemo is exactly 2688.22 kilometers (or 1,450 nautical miles) from the nearest land and there's no other point in ocean that far from the land. It's named after the fictional character captain Nemo from Jules Verne's novel Twenty Thousand Leagues Under the Sea published in 1870.
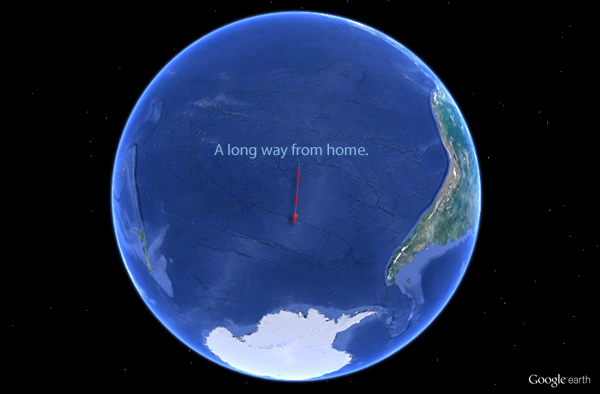
On a planet such as ours with complex landmass and ocean distribution having thousands of islands — some smaller than the size of a football field — finding such a point can be quite challenging. Further, such a point should be farthest not from one but three coastlines to fulfill the criteria of being farthest from "any land". Fortunately with modern day computational power at hands, finding such a point is not that difficult.
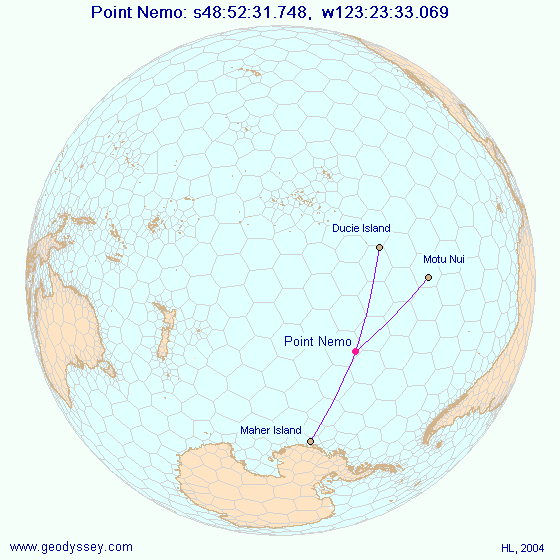
Point Nemo — with geographical coordinates of 48°52.6'S 123°23.6'W — is 2688.22 km away from the following three coastlines:
-
Ducie Island
-
Motu Nui
-
Maher Island
Ducie Island is a non-inhabited small C-shaped strip of land with a diameter of barely two kilometers. Motu Nui is also a small piece of land (less than 100 meter across) but it's near to a well-known bigger island: Rapa Nui or better known as Easter Island. It's the Rapa Nui island where you see those giant stone monolith statues: Moai. The 20 km wide volcanic island, Rapa Nui, has its own airport and is a developed tourist destination. The third one, Maher Island is a small piece of land on the outskirts of the larger Siple Island which is part of Antarctica.

So just in case you got stuck somewhere around Point Nemo and decide to come back, your best option is to head North towards Easter Island (of course 2688 km away), appreciate the historical Moai and get a plane back home.
Assignment
In this assignment we will work with maps that have been saved in a text file. The description of a map consists of a sequence of lines that all have the same length. Each line only contains hash symbols (#) that represent land and spaces that represent ocean. Each map has at least one piece of land and at least one piece of ocean. Below, you see an example map that has 25 lines containing 80 characters each.
## ##### ##### # ####
## #### ########## ####
# #### ############ ##
##### ##################
##### ########### ###
##### # ######
###
##### ###
######## #######
##################
### ##################
#### ### #################
##### ##### ### #################
############ ##### ###########
########### ### ###### ########
######### ####### ####### ######
##### ####### ##### ###
## ####### ###
## ####### # #
#### ####### ## #
##### ###### #### ### #
###### ####### ########### #### # #
###### ###### ########### ##### ### #
###### ### ####### ########## #### ###
##### #### ####### #### #####
A position on a map is described by a tuple $$(r, c)$$ where $$r$$ indicates the line on which the position is located and $$c$$ indicates which character on that line the position corresponds to. Lines are numbered top to bottom starting from zero, and characters on a line are numbered left to right starting from zero. As such, the position $$(0, 0)$$ is located in the top left corner of the map.
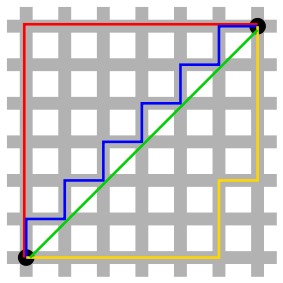
In this assignment we do not make use of the Euclidean distance to determine the distance $$d_M$$ between two positions $$(r_1, c_1)$$ and $$(r_2, c_2)$$, but we make use of the Manhattan distance. The latter is defined as the sum of the absolute differences of the coordinates of the two positions: \[ d_M((r_1, c_1), (r_2, c_2)) = |r_1 - r_2| + |c_1 - c_2|\] The name refers to the grid layout of most streets on the island of Manhattan, as fixed in a plan dating from 1811. The grid causes the shortest path a car or a pedestrian can take between two intersections in the borough to have length equal to the intersections' distance in Manhattan geometry (see the image below for an example).
Your task is to determine all positions on a given map that have the largest Manhattan distance to the nearest land. In order to do so, you have to define a class Map that supports at least the following methods:
-
An initialisation method that takes the location of a text file containing the description of a map.
-
A method isolation that takes two integers $$r$$ and $$c$$ that represent the coordinates $$(r, c)$$ of a position on the map. The method must return the Manhattan distance of the position $$(r, c)$$ to the nearest land.
-
A method nemo that takes no arguments. The method must return a set containing all positions on the map whose Manhattan distance to the nearest land is maximal.
-
A method __str__ that returns a string representation of the map. This string representation must be formatted the same way as the original representation of the map in the given text file, where all positions on the map whose Manhattan distance to the nearest land is maximal are represented by the letter X.
Remark: Apart from the fact that Earth is a sphere-like object, you should not treat maps as planar projections of a sphere. In determining distances between positions on a map, you should thus NOT consider the right end of the map to be connected to the left end of the map, or the bottom end of the map to be connected to the top end of the map.
Example
In the following interactive session, we assume the text file map.txt to be located in the current directory.
>>> map = Map('map.txt')
>>> map.isolation(0, 0)
1
>>> map.isolation(1, 2)
0
>>> map.isolation(2, 3)
2
>>> map.isolation(7, 78)
12
>>> map.isolation(11, 74)
12
>>> map.nemo()
{(7, 78), (11, 74), (8, 77), (10, 75), (6, 79), (9, 76)}
>>> print(map)
## ##### ##### # ####
## #### ########## ####
# #### ############ ##
##### ##################
##### ########### ###
##### # ######
### X
##### ### X
######## ####### X
################## X
### ################## X
#### ### ################# X
##### ##### ### #################
############ ##### ###########
########### ### ###### ########
######### ####### ####### ######
##### ####### ##### ###
## ####### ###
## ####### # #
#### ####### ## #
##### ###### #### ### #
###### ####### ########### #### # #
###### ###### ########### ##### ### #
###### ### ####### ########## #### ###
##### #### ####### #### #####
Epilogue
In June 1928, H.P. Lovecraft published a short science fiction story named The Call of Cthulhu, where Cthulhu is first mentioned. This fictional monstrous deity that arrived on Earth millions of years ago, is described as a colossal being that spends its time in the sunken city of R'lyeh, located near Point Nemo.
The virtual band Gorillaz
claims that Point Nemo is the location of their past headquarters, a
floating island made of junk known as Plastic Beach.