Op 26 november 2011 lanceerde NASA de rover Curiosity¹ vanop Cape Canaveral, om die op 6 augustus 2012 feilloos te laten landen op Aeolis Palus² in de Gale krater³ op Mars. Daarmee was het de vierde geslaagde landing van een Marsrover na deze van de Sojourner (4 juli 1977), de Spirit (10 juni 2003) en de Opportunity (7 juli 2003). Op 27 september 1997 ging het contact met de Sojourner verloren. Op 26 januari 2010 reed de Spirit zich vast in het zand na een afstand van 7.73 km te hebben afgelegd, en leeft sindsdien verder als een stationaire lander. Vandaag zijn dus enkel de Opportunity en de Curiosity nog mobiel. De Opportunity verbrak op 20 mei 2010 het record van langstdurende missie op het Marsoppervlak en op 28 juli 2014 het record van de langste afstand afgelegd op een niet-Aards oppervlak dat toen op 40.25 km stond.

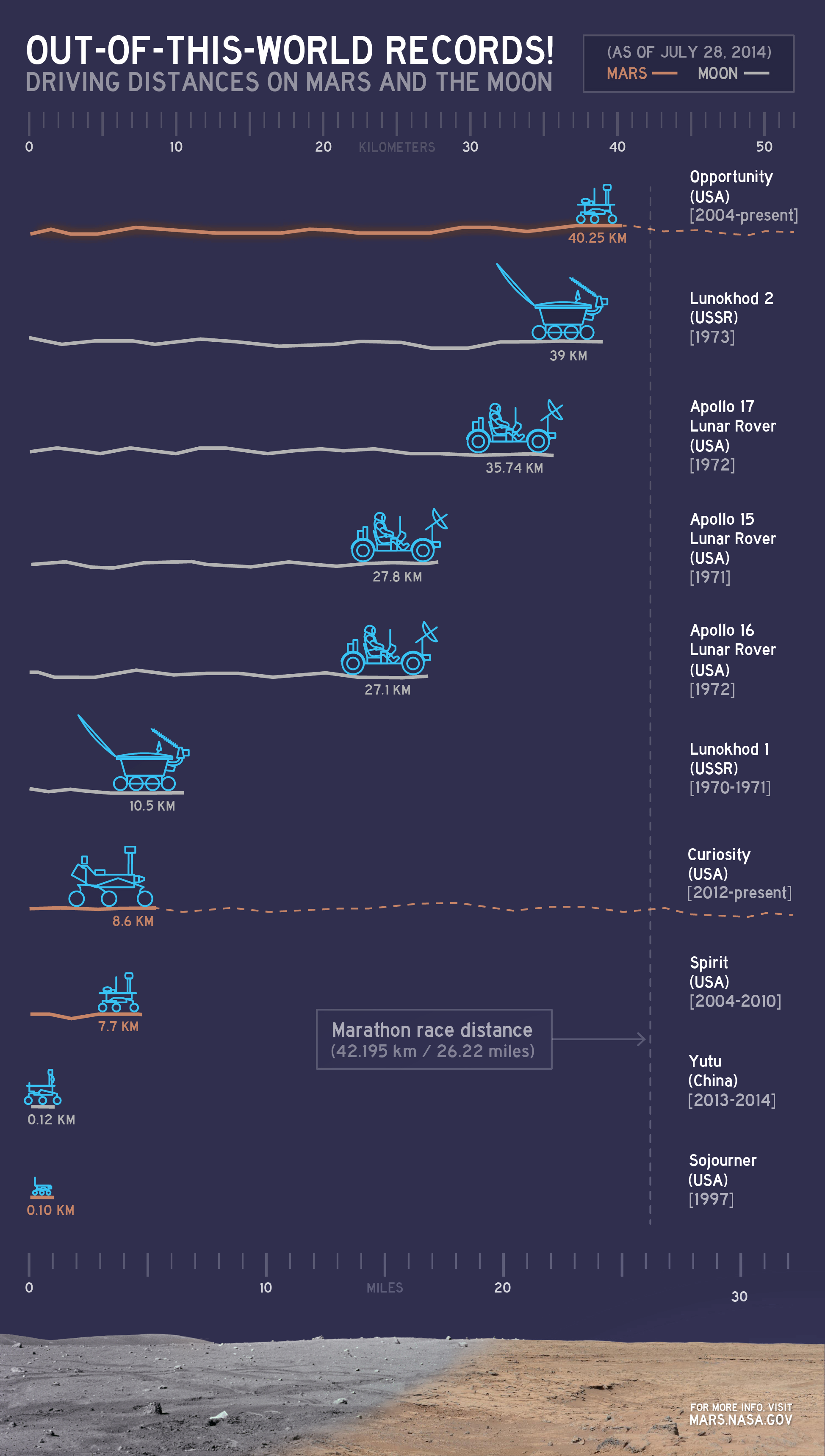
Mobiele Marsrovers⁴ hebben talloze voordelen ten opzichte van stationaire landers: ze kunnen grotere gebieden afspeuren, kunnen actief zoeken naar interessante objecten, kunnen zichzelf verplaatsen naar zonnige posities om hun batterijen op te laden, en ze leren ons heel wat over hoe voertuigen relatief autonoom kunnen bewegen op verafgelegen planeten. Om autonoom over het Marsoppervlak te kunnen bewegen en op zoek te gaan naar interessante objecten, worden Marsrovers gestuurd door software met kunstmatige intelligentie. Hierbij is het onder andere belangrijk om vormen te herkennen van objecten die zich rond de rover bevinden. Hieronder leren we je hoe dit in zijn werk gaat.

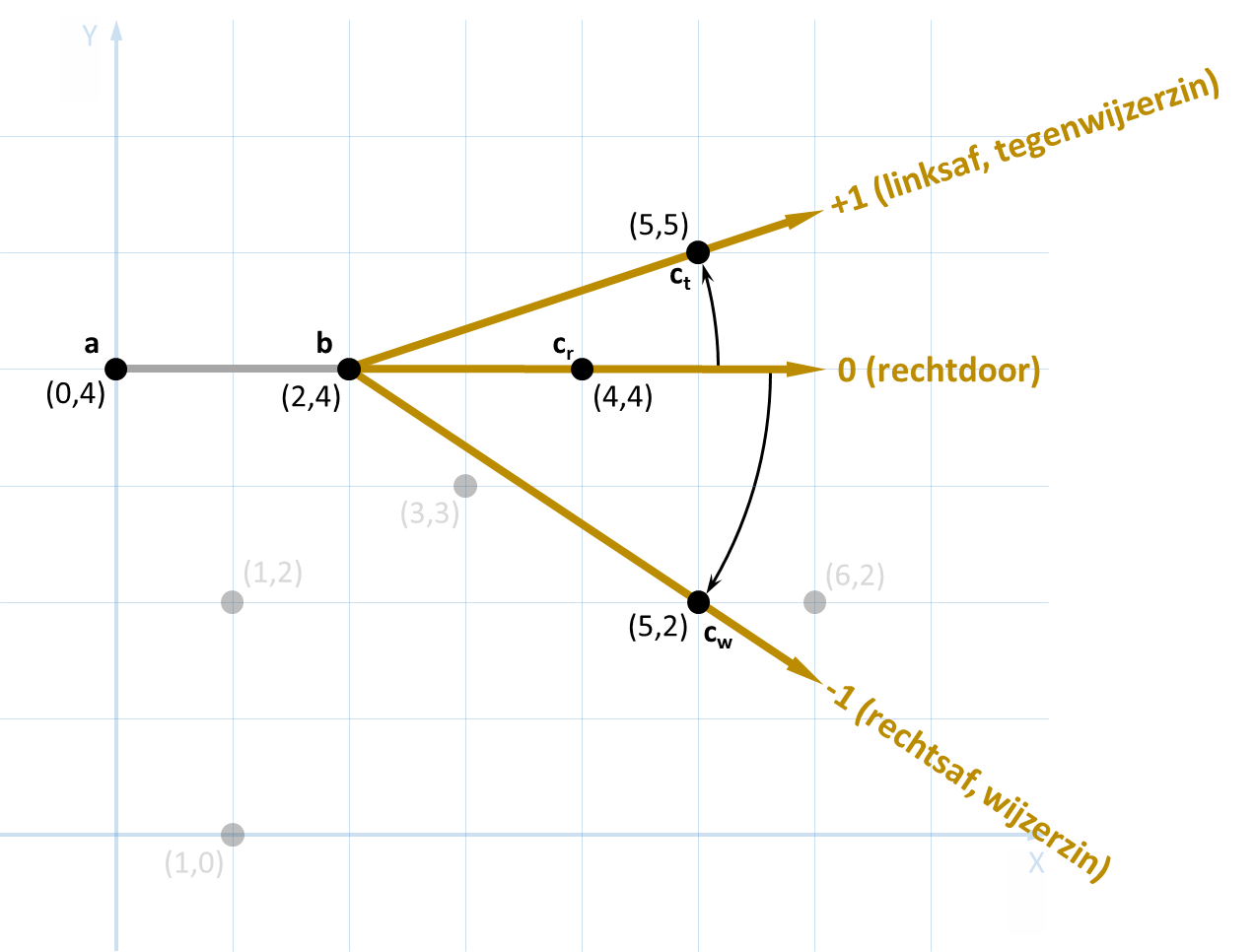
Voor de eenvoud werken we in het twee-dimensionale Euclidische vlak. Een punt in het vlak wordt voorgesteld door zijn coördinaten $$(x, y)$$, waarbij $$x, y \in \mathbb{Z}$$. Beschouw een pad dat loopt van een punt $$a = (x_a, y_a)$$ over een punt $$b = (x_b, y_b)$$ naar een punt $$c = (x_c, y_c)$$, en bepaal het resultaat van de volgende formule \[(x_b - x_a)(y_c - y_a) - (y_b - y_a)(x_c - x_a)\] Als deze waarde negatief is, dan draait het pad naar rechts (of in wijzerin). Als de waarde positief is, dan draait het pad naar links (of in tegenwijzerzin). Als de waarde gelijk is aan nul, dan gaat het pad rechtdoor.

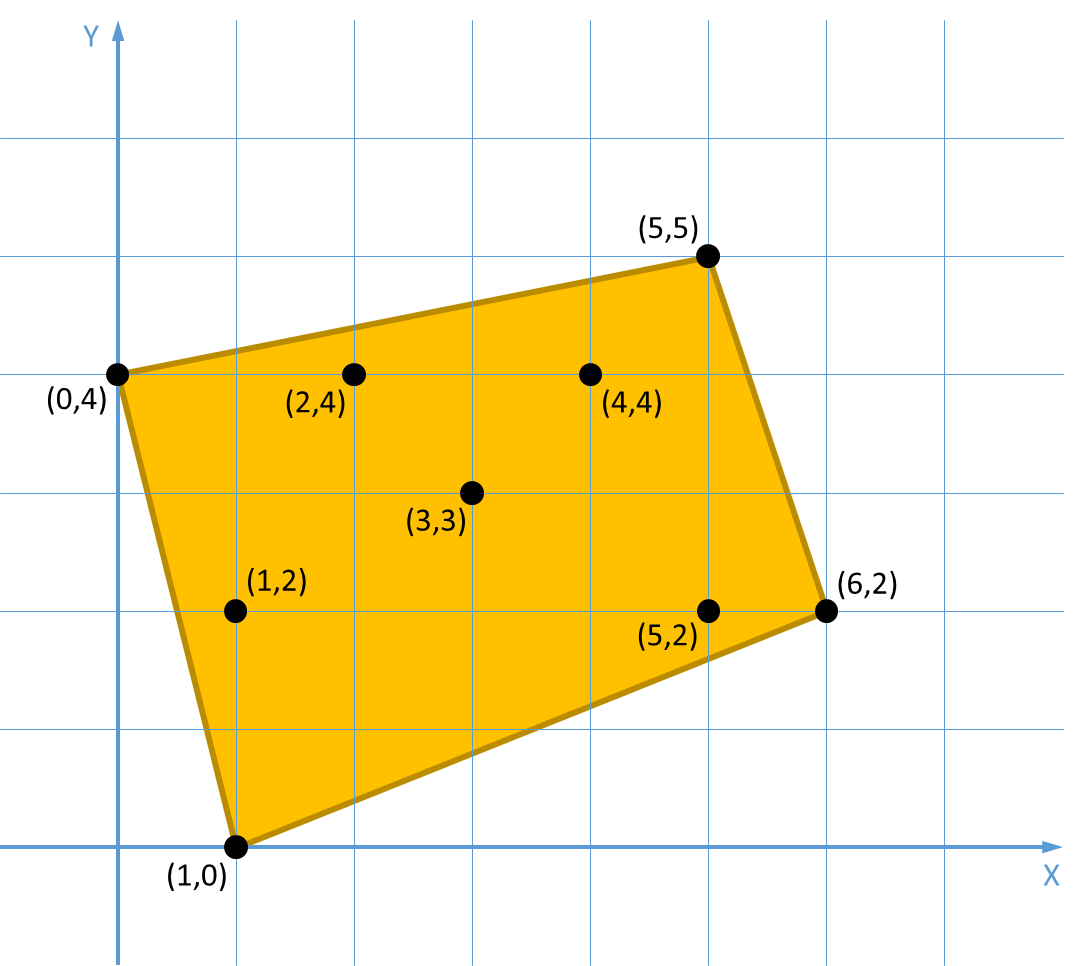
Beschouw een verzameling van $$n$$ punten $$\{p_1, p_2, \ldots, p_n\}$$ in het vlak, waarbij $$p_i = (x_i, y_i)$$ voor $$i = 1, 2, \ldots, n$$. Deze puntenverzameling stelt een object voor zoals het door de Marsrover wordt waargenomen. De contour van deze puntenverzameling kunnen we visueel voorstellen als de vorm die een elastiek aanneemt wanneer we hem rond al deze punten spannen.

Als we een punt $$a$$ op de contour kennen, dan moet voor het volgende punt $$b$$ op de contour (als we de contour in wijzerzin doorlopen) gelden dat alle andere punten van de puntenverzameling rechts van het pad van $$a$$ naar $$b$$ liggen (voor het punt $$a = (0, 4)$$ is dit het punt $$b = (5, 5)$$ in onderstaande figuur). We kunnen het punt dat volgt op het punt $$a$$ dus vinden door alle andere punten $$c$$ van de puntenverzameling te overlopen (dus zonder het punt $$a$$). Als het punt $$b$$ onze voorlopige kandidaat is als volgende punt op de contour, en het pad van $$a$$ over $$b$$ naar $$c$$ draait naar links, dan wordt $$c$$ onze nieuwe kandidaat. Als het pad van $$a$$ over $$b$$ naar $$c$$ rechtdoor loopt, dan wordt $$c$$ enkel onze nieuwe kandidaat als $$c$$ verder van $$a$$ ligt dan $$b$$. Hierbij wordt de afstand tussen twee punten $$(x_a, y_a)$$ en $$(x_b, y_b)$$ bepaald als $$\sqrt{(x_a - x_b)^2 + (y_a - y_b)^2}$$. Als we op die manier alle punten uit de puntenverzameling hebben overlopen (behalve het punt $$a$$ zelf), dan hebben we met de kandidaat die we op het einde overhouden het punt gevonden dat op de contour volgt op het punt $$a$$ als we de punten van de contour in wijzerin overlopen.

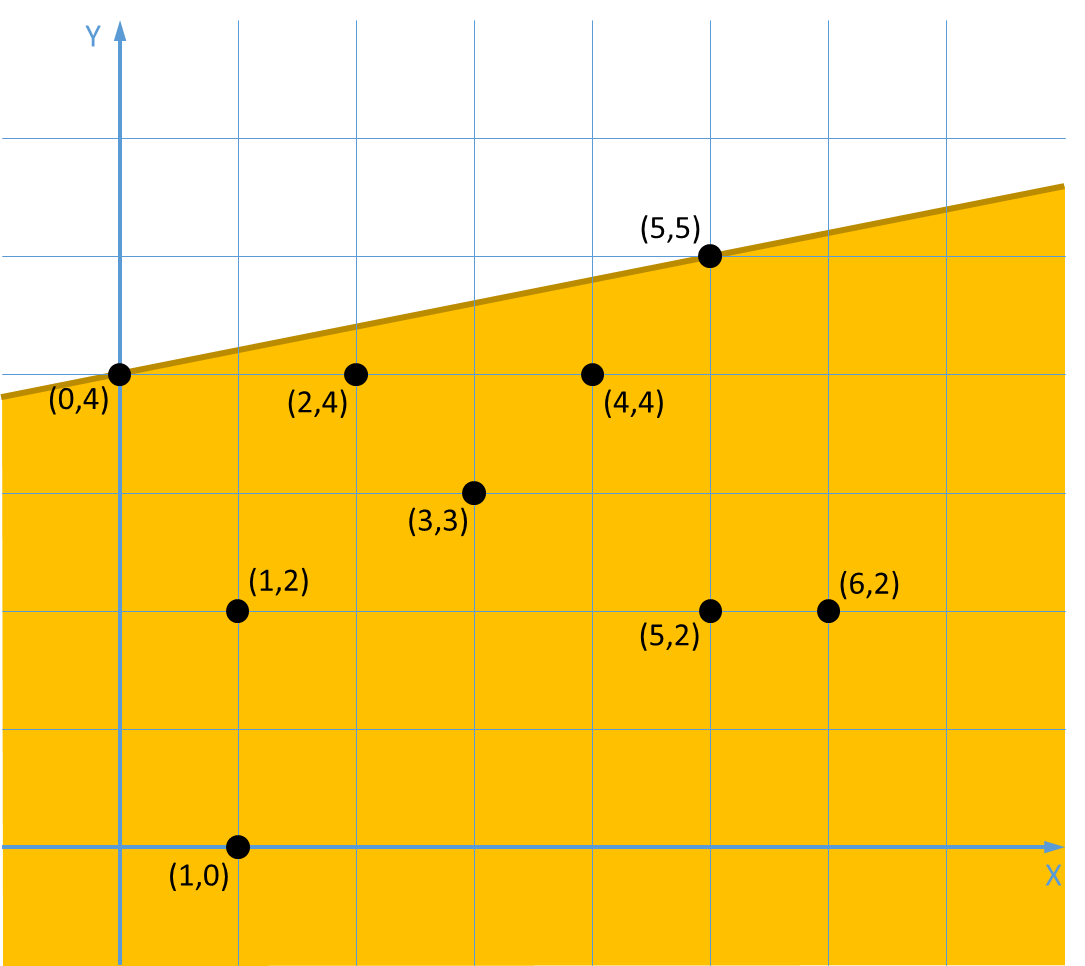
We kunnen nu als volgt te werk gaan om de contour van een gegeven puntenverzameling te bepalen. Het eerste punt op de contour is het meest linkse punt van de puntenverzameling. Indien er meerdere punten zijn die links van alle andere punten liggen, dan nemen we daarvan het onderste punt. Voor de puntenverzameling uit bovenstaande figuur is dit het punt $$(0, 4)$$. Daarna bepalen we steeds het volgende punt, totdat we uiteindelijk terug bij het oorspronkelijke punt uitkomen.

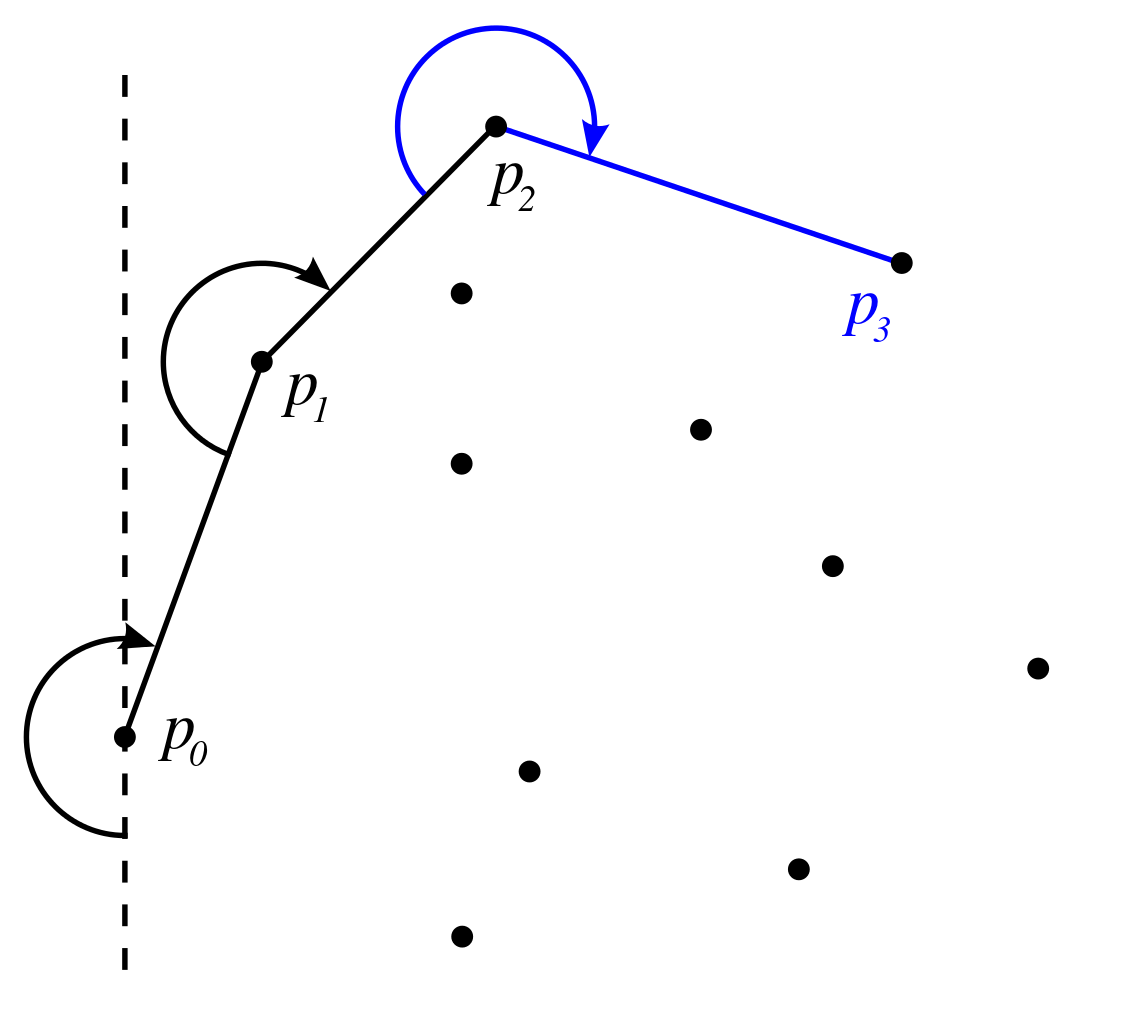
Op die manier worden de opeenvolgende punten van de contour in wijzerzin doorlopen. Als we in bovenstaande omschrijving alle voorkomens van "rechts" vervangen door "links", dan worden de punten van de contour in tegenwijzerzin doorlopen.

Opgave

In deze opgave stellen we een punt in het twee-dimensionale Euclidische vlak voor als een tuple $$(x, y)$$, met $$x, y \in \mathbb{Z}$$. Een puntenverzameling stellen we voor als een lijst, een tuple of een verzameling van punten, waarbij we ervan uitgaan dat alle punten in de puntenverzameling verschillend zijn. Gevraagd wordt:

• Schrijf een functie draaien waaraan drie verschillende punten $$a$$, $$b$$ en $$c$$ moeten doorgegeven worden. De functie moet -1, 0 of 1 teruggeven als het pad $$a$$ over $$b$$ naar $$c$$ respectievelijk naar rechts (wijzerzin), rechtdoor, of naar links (tegenwijzerzin) draait. De functie moet een AssertionError opwerpen met de boodschap drie punten moeten verschillend zijn indien minstens twee van de drie gegeven punten gelijk zijn.

• Schrijf een functie volgende waaraan een punt en een puntenverzameling moeten doorgegeven worden. De functie mag ervan uitgaan dat het gegeven punt tot de gegeven puntenverzameling behoort en op diens contour ligt. De functie heeft ook nog een derde optionele parameter wijzerzin waaraan een Booleaanse waarde kan doorgegeven worden (standaardwaarde: True). De functie moet het punt op de contour van de gegeven puntenverzameling teruggeven dat volgt op het gegeven punt. Hierbij worden de punten op de contour in wijzerzin doorlopen als de waarde True werd doorgegeven aan de parameter wijzerzin. Anders worden ze in tegenwijzerzin doorlopen.

• Schrijf een functie contour waaraan een puntenverzameling moet doorgegeven worden. De functie heeft ook nog een tweede optionele parameter wijzerzin waaraan een Booleaanse waarde kan doorgegeven worden (standaardwaarde: True). De waarde die aan deze parameter wordt doorgegeven geeft aan of de punten van de contour van de gegeven puntenverzameling in wijzerzin (True) of in tegenwijzerzin (False) moeten doorlopen worden. De functie moet een lijst met de opeenvolgende punten op de contour van de gegeven puntenverzameling teruggeven, te beginnen met het meest linkse (onderste) punt van de puntenverzameling.

Voorbeeld

>>> draaien((0, 4), (2, 4), (5, 2))
-1
>>> draaien((0, 4), (2, 4), (4, 4))
0
>>> draaien((0, 4), (2, 4), (5, 5))
1
>>> draaien((0, 4), (2, 4), (0, 4))
Traceback (most recent call last):
AssertionError: drie punten moeten verschillend zijn

>>> punten = ((3, 3), (0, 4), (4, 4), (1, 0), (6, 2), (2, 4), (5, 5), (1, 2), (5, 2))

>>> volgende((0, 4), punten)
(5, 5)
>>> volgende((5, 5), punten, True)
(6, 2)
>>> volgende((6, 2), punten, wijzerzin=True)
(1, 0)
>>> volgende((1, 0), punten)
(0, 4)

>>> volgende((0, 4), punten, False)
(1, 0)
>>> volgende((1, 0), punten, wijzerzin=False)
(6, 2)
>>> volgende((6, 2), punten, False)
(5, 5)
>>> volgende((5, 5), punten, wijzerzin=False)
(0, 4)

>>> contour(punten)
[(0, 4), (5, 5), (6, 2), (1, 0)]
>>> contour(punten, wijzerzin=False)
[(0, 4), (1, 0), (6, 2), (5, 5)]

Epiloog

De Marsrover Curiosity is voorzien van zes wielen met een doorsnede van 50 cm. Elk wiel is voorzien van groeven en wordt afzonderlijk bestuurd en aangedreven, waardoor de rover makkelijk kan klimmen in zacht zand en over rotsen kan klauteren. Op elk wiel is ook een patroon van gaten aangebracht dat helpt om tractie te behouden, maar dat bovendien ook een specifiek spoor achterlaat in het zand van Mars. Het patroon in dit spoor wordt door boordcamera's gebruikt om de afgelegde afstand te kunnen inschatten. Het patroon van brede en smalle gaten is morsecode voor JPL (·--- ·--· ·-··), waardoor de rover bij elke omwenteling van zijn wielen een kleine stempel achterlaat die verwijst naar de plaats waar hij gemaakt werd: het Jet Propulsion Lab.