Wiskundig kan men bewijzen dat de som van de omgekeerden van alle driehoeksgetallen gelijk is aan 2, met andere woorden:
\[\mathsf{ \dfrac{1}{1}+\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\ldots = 2}\]Hierbij zijn 1, 3, 6, 10, … driehoeksgetallen omdat je ze kan vormen door het aantal cirkels in een driehoek te stapelen.
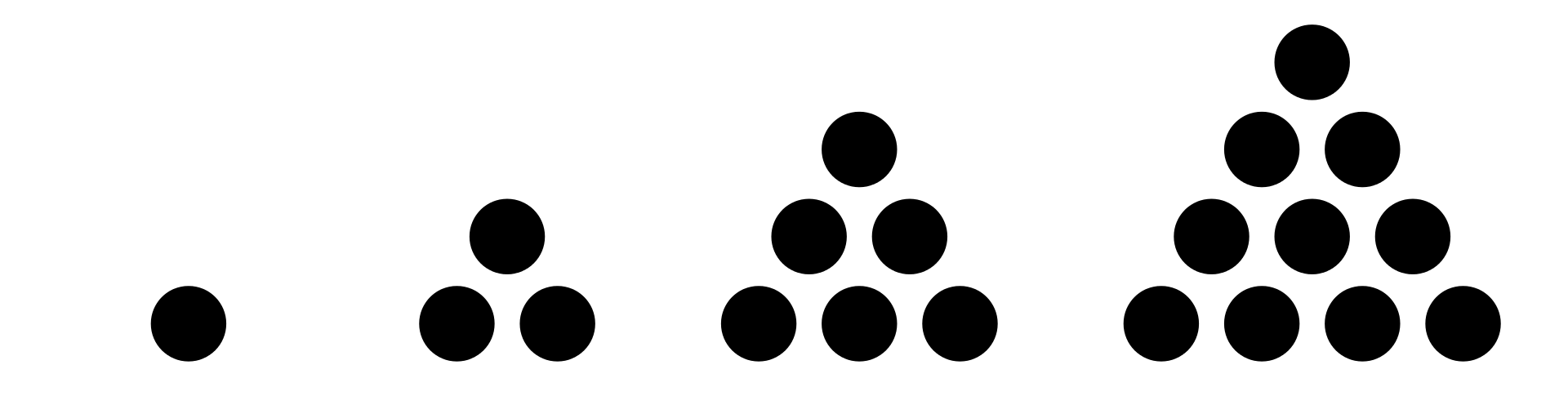
Bovenstaande som kan herschreven worden in de volgende vorm:
\[\mathsf{ \dfrac{1}{1}+\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\ldots = \sum_{n=1}^\infty \dfrac{2}{n\cdot (n+1)}}\]Gevraagd
- Maak een functie
som_driehoek(aantal)waarbijaantalhet aantal termen uit de som voorstelt. Zo geldt datsom_driehoeks(3)overeenkomt met
- Laat R het resultaat van het product afronden op 6 cijfers na de komma.
Voorbeelden
De eerste 3 termen van de som berekenen resulteert in:
> som_driehoek(3)
[1] 1.5
De eerste 10 termen van de som berekenen resulteert in:
> som_driehoek(10)
[1] 1.818182