Make a stack that has an equal amount of red and black cards. Shuffle the cards and deal them in pairs. If the two cards are red, place them on top of the red stack. If the two cards are black, place them on top of the black stack. Discard the two cards if they form a red-black pair, irrespective of their order.
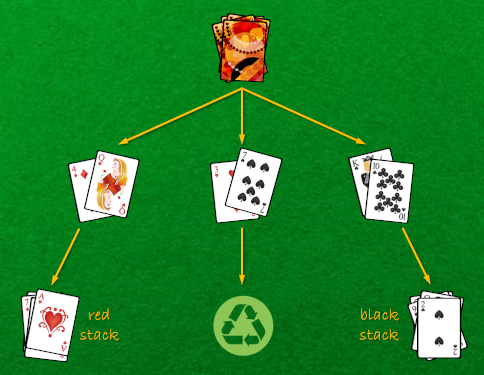
If all cards have been dealt, you'll find that the number of red cards in the red stack always equals the number of black cards in the black stack. Can you explain why?
Assignment
A standard card deck includes 52 different cards, evenly distributed over four suits: 13 clubs (♣), 13 diamonds (♦), 13 hearts (♥) and 13 spades (♠). Clubs and spades are black, whereas diamonds and hearts are red. Each suit includes thirteen ranks: two through ten (with each card depicting that many symbols of its suit), jack, queen, king (each depicted with a symbol of its suit) and ace (depicting a single symbol of its suit). Commercial card decks may also include anywhere from one to six jokers, but we do not take these into account here.
Each card of a standard 52-card deck is represented by a string (str) that contains the rank of the card, followed by its suit:
-
ranks: 2, 3, 4, 5, 6, 7, 8, 9, 10, J (jack), Q (queen), K (king) and A (ace)
-
suits: C (clubs; ♣), D (diamonds; ♦), H (hearts; ♥) and S (spades; ♠)
As such, the ace of spades is for example represented as AS, the ten of hearts as 10H and the king of clubs as KC.
A sequence representation of a stack of cards is a list (list) or a tuple (tuple) containing the representations of the consecutive cards in the stack, where the top card of the stack is the first element. A stack of cards does not necessarily contain all 52 cards of a standard deck, but a card may never occur more than once in the stack.
Define a class Stack that can be used to represent stacks of cards. A sequence representation of a stack of cards must be passed when creating an object of the class Stack, which requires explicit checking that the given stack meets the following conditions:
-
the stack is represented as a list (list) or a tuple (tuple)
-
each element of the stack is a valid string representation (str) of a card
-
no card occurs more than once in the stack
An AssertionError must be raised with the message invalid stack if the given stack does not meet these conditions.
If an object of the class Stack is passed to the built-in function len, the function must return the number of cards (int) in the stack. If an object of the class Stack is passed to the built-in function str, the function must return a string (str) containing the string representations of the individual cards, listed from top to bottom and separated by spaces. If an object of the class Stack is passed to the built-in function repr, the function must return a string (str) containing a Python expression that creates a new object of the class Stack that has the same state as the given object, where a list (list) is used as the sequence representation of the stack of cards. In addition, the class Stack must at least support the following methods:
-
A method draw that takes an integer $$n \in \mathbb{N}$$ (int), where $$n$$ may not exceed the number of cards in the stack. If $$n$$ exceeds the number of cards in the stack, an AssertionError must be raised with the message invalid number of cards. Otherwise, the method must remove the top $$n$$ cards from the stack and return them as a new stack (Stack). The cards in the new stack keep the same order as in the original stack.
-
A method deal that takes no arguments. The method must raise an AssertionError with the message odd number of cards if the number of cards in the stack is odd. Otherwise, the method must return a tuple (tuple) containing the red stack (Stack) and the black stack (Stack) obtained after dealing the cards in the original stack according to the procedure outlined in the introduction. When placing a pair of cards on top of the red/black stack, they must keep the same order as in the original stack.
When dealing, two cards must be drawn from the original stack and placed on the red/black stack in their original order. There should be no more cards in the original stack after dealing has finished.
Make sure the + operator can be used to join two stacks (Stack). The result is a new stack (Stack), where the cards from the first stack (left-hand side of the + operator) are on top of the cards from the second stack (right-hand side of the + operator). The + operator should not change the state of the original stacks.
Example
>>> stack = Stack(('5S', 'QC', '8S', 'QD', 'JC', '10C', '4H', '4S', '2D', '7S', '3S', '3C', '4D', '7H', '3H', '5H', 'KD', '6C', '2S', '9C'))
>>> len(stack)
20
>>> stack.draw(3)
Stack(['5S', 'QC', '8S'])
>>> stack
Stack(['QD', 'JC', '10C', '4H', '4S', '2D', '7S', '3S', '3C', '4D', '7H', '3H', '5H', 'KD', '6C', '2S', '9C'])
>>> len(stack)
17
>>> stack.draw(5)
Stack(['QD', 'JC', '10C', '4H', '4S'])
>>> print(stack)
2D 7S 3S 3C 4D 7H 3H 5H KD 6C 2S 9C
>>> len(stack)
12
>>> stack.draw(42)
Traceback (most recent call last):
AssertionError: invalid number of cards
>>> red_stack, black_stack = stack.deal()
>>> red_stack
Stack(['3H', '5H', '4D', '7H'])
>>> black_stack
Stack(['2S', '9C', '3S', '3C'])
>>> stack
Stack([])
>>> len(red_stack) == len(black_stack)
True
>>> red_stack + black_stack
Stack(['3H', '5H', '4D', '7H', '2S', '9C', '3S', '3C'])
>>> red_stack + red_stack
Traceback (most recent call last):
AssertionError: invalid stack
Epilogue
If you're still thinking why the red stack always has the same number of cards as the black stack, think of it in the following way. Because the cards that are put aside are paired by color, the remaining cards must be divided equally between red and black. So when all cards have been dealt, both stacks will always have the same number of cards.
The same reasoning leads you to the answer of the following alcohol problem. Fill one glass with wine and another with water. Transfer a teaspoonful of wine from the first glass into the second. Then transfer a teaspoonful of that mixture back into the first glass. Now, is there more wine in the water or water in the wine?
Most people will predict it's the former, but in fact the two quantities will always be the same. Can you see why?