In astronomy, Planck's law  describes the electromagnetic radiation emitted by a black body1 in the thermal equilibrium at a definite temperature: \[\rho(T,\lambda) = \frac{8\pi hc}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda k T}}- 1}\] Here, $$T$$ is the temperature (in Kelvin), $$\lambda$$ is the wavelength (in metre), $$h$$ is the constant of Planck ($$6,62608 \times 10^{-34}$$ Js), $$c$$ the light speed ($$2,99792458 \times 10^8$$ ms$$^{-1}$$), and $$k$$ is the constant of Boltzmann ($$1,38066 \times 10^{-23}$$ JK$$^{-1}$$).

Hint: Compare the output of your program with the picture below (source: Wikipedia2):

wet van Planck
Planck's law (colored curves) accurately describes black body radiation, with a representation that states that electromagnetic radiation is sent out by quanta3. This law successfully solves the ultraviolet catastrophe4 — a major issue in classic physics — where it was of great importance for the development of quantum mechanics5.

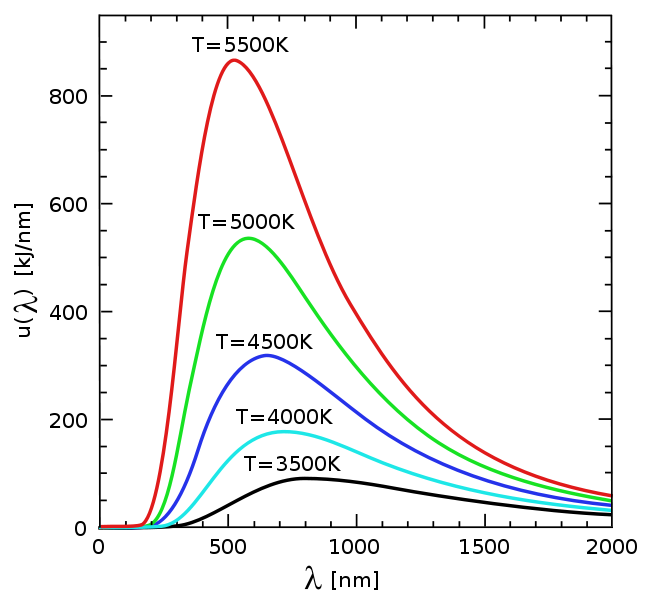
Input

The input consists of $$t$$ test cases ($$t \leq 50$$). The first line of the input contains an integer $$t$$. Then, $$t$$ lines follow that describe the different test cases. For every test case, the input contains two lines. The first line contains a given temperature $$T$$ expressed in Kelvin. The second line contains a given wavelength $$\lambda$$ expressed in micrometre (1 micrometre = $$10^{-6}$$ metre).

Output

For every test case, the energy density $$\rho$$ in SI units (this is Joule per m$$^4$$) that corresponds with the given temperature $$T$$ and wavelength $$\lambda$$.

Example

Input:

5
5500
0.5
4500
0.5
3500
0.5
5000
1.0
4000
1.0

Output:

858255.480667
267354.545955
42955.5563284
297696.258875
140690.424377