What number comes at the position of the question mark?
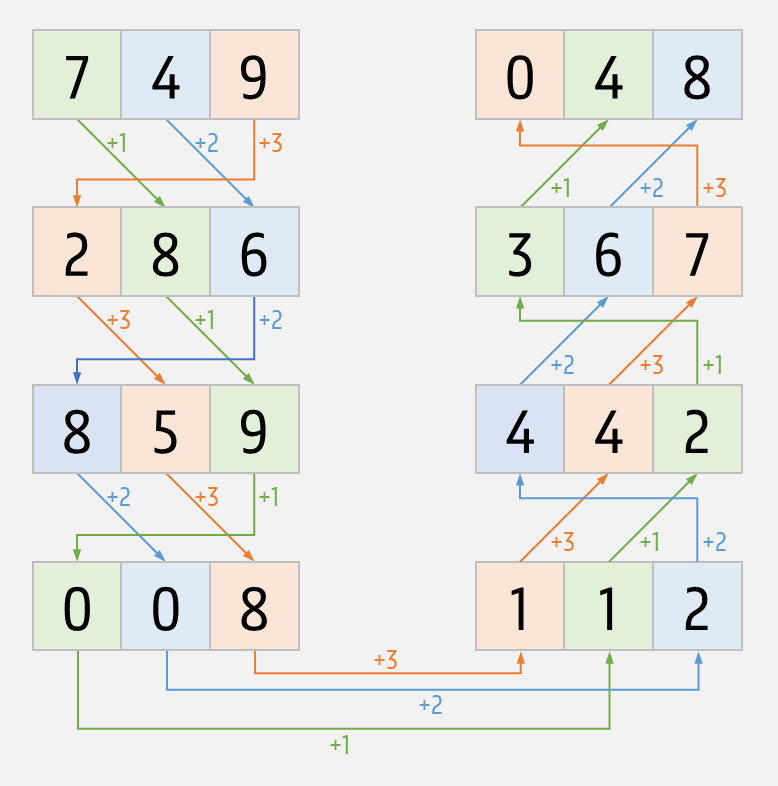
749, 286, 859, 008, 112, 442, 367, ?, …
The next number in the sequence is 048. This number sequence is an example of an arithmetic progression of 749 with shifts 123.
Assignment
We represent an $$n$$-digit number $$d = d_1d_2\ldots d_n$$ as a string (str) with $$n$$ digits.
For two $$n$$-digit numbers $$d = d_1d_2\ldots d_n$$ and $$s = s_1s_2\ldots s_n$$ the arithmetic progression of $$d$$ with shifts $$s$$ is a number sequence that starts with the number $$d$$. Each next number in the arithmetic progression is derived from the previous number through a progression step.
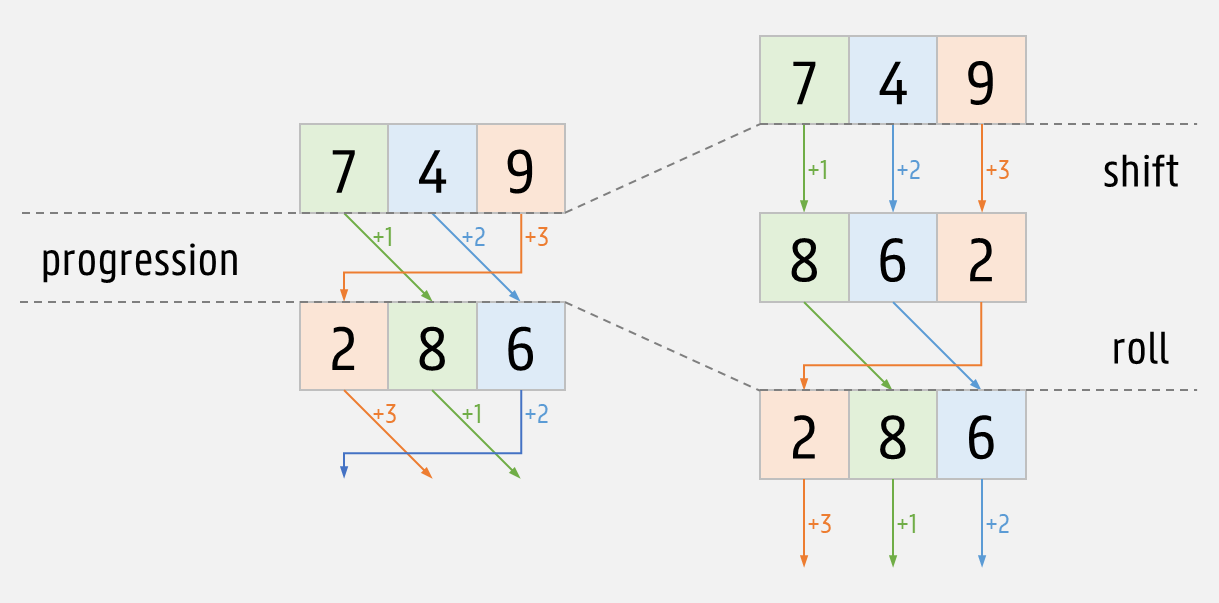
In a progression step we first shift the digits of number $$d = d_1d_2\ldots d_n$$ with shifts $$s = s_1s_2\ldots s_n$$. This yields a new $$n$$-digit number $$d' = d'_1d'_2\ldots d'_n$$ where $$d'_i = (d_i + s_i)\!\!\!\!\mod{10}$$ for $$i = 1, 2, \ldots, n$$ and $$\text{mod}$$ is the modulo operation that computes the remainder after integer division. Then we roll the number $$d'$$ to the right by moving all of its digits one position to the right and putting its last digit in front. This yields a new $$n$$-digit number $$d'' = d'_nd'_1d'_2\ldots d'_{n-1}$$.
The progression step determines that the number $$d$$ is followed by the number $$d''$$ in the arithmetic progression. However, to determine the successor of the number $$d''$$ in the arithmetic progression, we will not use the shifts $$s$$ in the next progression step but we also roll those shifts to the right. As a result, the next progression step will work with shifts $$s'' = s_ns_1s_2\ldots s_{n-1}$$.
For two $$n$$-digit numbers $$d$$ and $$s$$ the arithmetic progression of $$d$$ with shifts $$s$$ is cyclic. The number of progression steps after which the sequence returns to the number $$d$$ is called the period of the arithmetic progression. For example, in the arithmetic progression of 749 with shifts 123, we return to the number 749 after 30 progression steps. This is also the maximum period, because the period is always less than or equal to $$10 \times n$$ for an $$n$$-digit number. However, shorter periods are also possible. For example, the arithmetic progression of 749 with shifts 154 has a period of 7, and with shifts 758 we even get the number 749 after a single progression step.

Your task:
-
Write a function roll that takes an $$n$$-digit number $$d = d_1d_2\ldots d_n$$. The function must return the $$n$$-digit number $$d_nd_1d_2\ldots d_{n-1}$$ that results from moving all digits of $$d$$ one position to the right and putting its last digit in front.
-
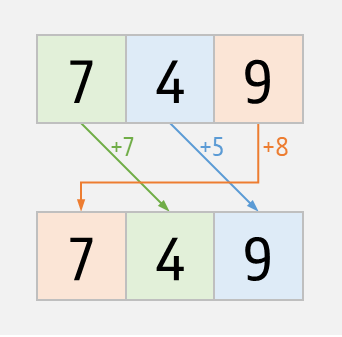
Write a function shift that takes two $$n$$-digit numbers $$d = d_1d_2\ldots d_n$$ and $$s = s_1s_2\ldots s_n$$. The function must return the $$n$$-digit number $$d'_1d'_2\ldots d'_n$$ where $$d'_i = (d_i + s_i)\!\!\!\!\mod{10}$$ for $$i = 1, 2, \ldots, n$$ and $$\text{mod}$$ is the modulo operation that computes the remainder after integer division.
-
Write a function progression that takes three arguments: i) an $$n$$-digit number $$d = d_1d_2\ldots d_n$$, ii) an $$n$$-digit number $$s = s_1s_2\ldots s_n$$ iii) and an integer $$m \in \mathbb{N}$$ (int). The function must return the $$n$$-digit number that is obtained after $$m$$ progression steps in the arithmetic progression of $$d$$ with shifts $$s$$.
-
Write a function period that takes two $$n$$-digit numbers $$d = d_1d_2\ldots d_n$$ and $$s = s_1s_2\ldots s_n$$. The function must return the period (int) of the arithmetic progression of $$d$$ with shifts $$s$$.
Example
>>> roll('749')
'974'
>>> roll('48839')
'94883'
>>> shift('749', '123')
'862'
>>> shift('52736', '97563')
'49299'
>>> progression('749', '123', 1)
'286'
>>> progression('749', '123', 2)
'859'
>>> progression('749', '123', 3)
'008'
>>> progression('749', '123', 30)
'749'
>>> progression('52736', '97563', 1)
'94929'
>>> progression('52736', '97563', 2)
'52367'
>>> progression('52736', '97563', 3)
'21523'
>>> progression('52736', '97563', 9)
'52736'
>>> period('749', '123')
30
>>> period('749', '154')
7
>>> period('749', '758')
1
>>> period('52736', '97563')
9
>>> period('416275', '869241')
21