Lee Sallows construeerde deze zelfbeschrijvende rechthoekige betegeling: het rooster inventariseert zichzelf door de 70 letters en de 14 spaties horizontaal en verticaal te ordenen in 14 zinnen die een oplijsting van de inhoud geven.
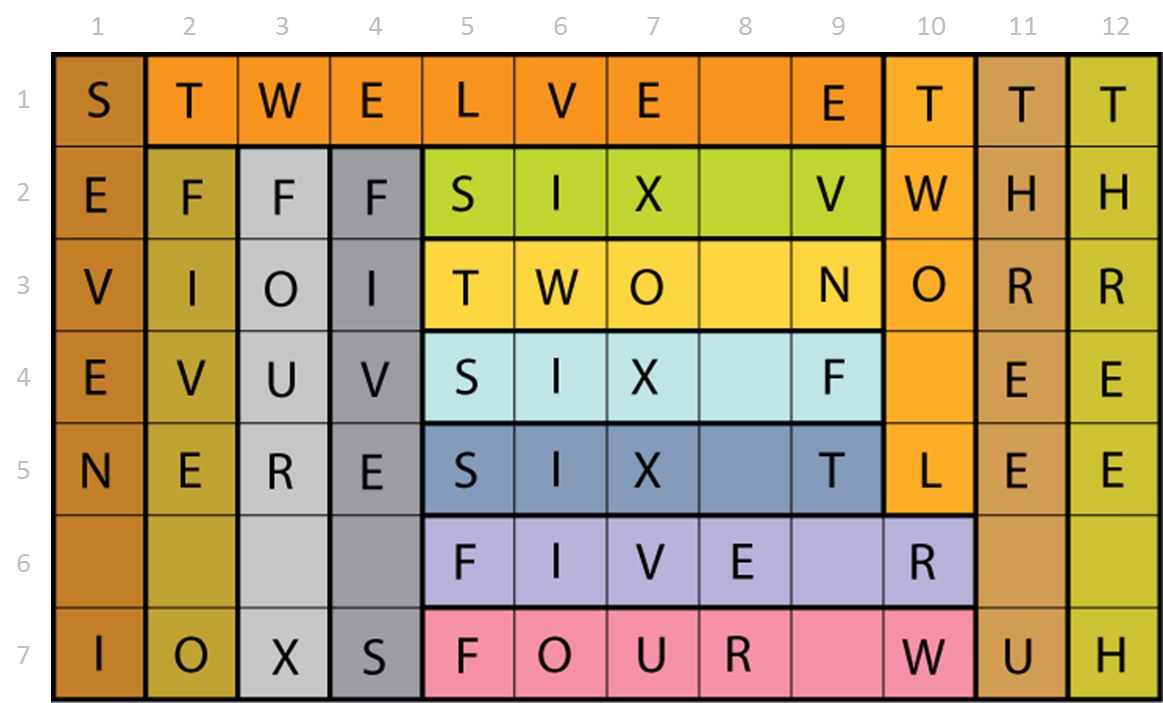
Bonus: De twee zinnen die samenkomen in de rechterbovenhoek corresponderen met de afmetingen van de rechthoek ($$7 \times 12$$) en de voornaam van de auteur is ook opgenomen.
Opgave
Definieer een klasse Inventaris waarmee horizontaal en verticaal zinnen in een rechthoekig rooster kunnen geplaatst worden. Deze zinnen geven aan hoe vaak elke letter in het rooster voorkomt. Bij het aanmaken van objecten van de klasse Inventaris moeten twee getallen $$n$$ en $$m$$ (int) doorgegeven worden, waarbij $$n \in \mathbb{N}_0$$ het aantal rijen van het rooster aangeeft en $$m \in \mathbb{N}_0$$ het aantal kolommen. De rijen van het rooster worden van boven naar onder genummerd en de kolommen van links naar rechts, telkens vanaf één.
Zorg ervoor dat de ingebouwde functie print kan gebruikt worden om de stringvoorstelling van een object van de klasse Inventaris uit te schrijven. Deze stringvoorstelling geeft elke rij van het rooster weer op een afzonderlijke regel. Elke cel wordt voorgesteld door één van de volgende karakters:
-
de hoofdletter die in de cel werd ingevuld
-
een koppelteken (-) als er een spatie in de cel werd ingevuld
-
een hekje (#) als er nog niets in de cel werd ingevuld
De klasse Inventaris moet minstens de volgende methoden ondersteunen:
-
Een methode plaats waarmee een zin in het rooster kan geplaatst worden die aangeeft dat de hoofdletter $$u$$ in het rooster $$o$$ keer zal voorkomen als het rooster volledig gevuld is. Aan deze methode moeten drie argumenten doorgegeven worden: i) de hoofdletter $$u$$ (str), ii) het getal $$o \in \mathbb{N}$$ (int, $$0 < o \leq 12$$) en iii) een omschrijving (str) die aangeeft waar de zin in het rooster moet geplaatst worden. De zin bestaat uit de benaming van het getal $$o$$, gevolgd door een spatie en de hoofdletter $$u$$. Hierbij wordt gebruikgemaakt van de volgende Engelstalige benamingen van de natuurlijke getallen:
ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE TEN ELEVEN TWELVE
Om de positie van de zin in het rooster te beschrijven wordt gebruikgemaakt van het formaat dr:c. Hierbij zijn de getallen $$r$$ en $$c$$ respectievelijk het rij- en kolomnummer van de cel waarin de eerste letter van de zin moet ingevuld worden, en is $$d$$ een hoofdletter die de richting aangeeft waarin de letters van de zin moeten ingevuld worden: H voor horizontaal (zin leest van links naar rechts) en V voor verticaal (zin leest van boven naar onder).
De methode moet achtereenvolgens de volgende controles uitvoeren op de gegeven argumenten. Als een controle faalt dan mag de methode niets invullen in het rooster en moet ze een AssertionError opwerpen met de boodschap die gegeven wordt aan het begin van de omschrijving van elke controle.
-
ongeldige letter: het eerste argument moet een string zijn die bestaat uit één hoofdletter
-
letter reeds gebruikt: voor elke hoofdletter mag hoogstens één zin in het rooster geplaatst worden
-
ongeldige positie: de omschrijving van de positie moet gebeuren volgens het opgegeven formaat en de zin moet op die positie in het rooster kunnen geplaatst worden (zonder evenwel rekening te houden met cellen die reeds ingevuld zijn)
-
positie reeds gebruikt: de karakters van de zin mogen enkel ingevuld worden in cellen die nog niet ingevuld waren
-
Een methode opgelijste_voorkomens waaraan geen argumenten kunnen doorgegeven worden. De methode moet een dictionary teruggeven die voor elke zin die de methode plaats in het rooster geplaatst heeft de hoofdletter $$u$$ (eerste argument) afbeeldt op het getal $$o$$ (tweede argument).
-
Een methode waargenomen_voorkomens waaraan geen argumenten kunnen doorgegeven worden. De methode moet een dictionary teruggeven die elke hoofdletter die in het rooster geplaatst werd afbeeldt op het aantal voorkomens van die hoofdletter in het rooster.
-
Een methode volledig waaraan geen argumenten kunnen doorgegeven worden. De methode moet een Booleaanse waarde teruggeven die aangeeft of elke cel van het rooster ingevuld werd met een hoofdletter of een spatie.
-
Een methode zelfbeschrijvend waaraan geen argumenten kunnen doorgegeven worden. De methode moet een Booleaanse waarde teruggeven die aangeeft of het rooster volledig ingevuld werd met zinnen die aangeven hoe vaak elke hoofdletter in het rooster voorkomt.
Voorbeeld
>>> inventaris = Inventaris(7, 12)
>>> print(inventaris)
############
############
############
############
############
############
############
>>> inventaris.opgelijste_voorkomens()
{}
>>> inventaris.waargenomen_voorkomens()
{}
>>> print(inventaris.plaats('N', 2, 'H3:5'))
############
############
####TWO-N###
############
############
############
############
>>> inventaris.opgelijste_voorkomens()
{'N': 2}
>>> inventaris.waargenomen_voorkomens()
{'N': 1, 'O': 1, 'T': 1, 'W': 1}
>>> print(inventaris.plaats('.', 2, 'H4:5'))
Traceback (most recent call last):
AssertionError: ongeldige letter
>>> print(inventaris)
############
############
####TWO-N###
############
############
############
############
>>> print(inventaris.plaats('N', 2, 'H4:5'))
Traceback (most recent call last):
AssertionError: letter reeds gebruikt
>>> print(inventaris)
############
############
####TWO-N###
############
############
############
############
>>> print(inventaris.plaats('S', 5, 'V2:4'))
############
###F########
###ITWO-N###
###V########
###E########
###-########
###S########
>>> inventaris.opgelijste_voorkomens()
{'N': 2, 'S': 5}
>>> inventaris.waargenomen_voorkomens()
{'E': 1, 'F': 1, 'I': 1, 'N': 1, 'O': 1, 'S': 1, 'T': 1, 'V': 1, 'W': 1}
>>> print(inventaris.plaats('E', 12, 'H1:2').plaats('R', 5, 'H6:5').plaats('W', 4, 'H7:5'))
#TWELVE-E###
###F########
###ITWO-N###
###V########
###E########
###-FIVE-R##
###SFOUR-W##
>>> inventaris.plaats('X', 6, 'H13:2')
Traceback (most recent call last):
AssertionError: ongeldige positie
>>> print(inventaris)
#TWELVE-E###
###F########
###ITWO-N###
###V########
###E########
###-FIVE-R##
###SFOUR-W##
>>> inventaris.plaats('X', 6, 'H3:2')
Traceback (most recent call last):
AssertionError: positie reeds gebruikt
>>> print(inventaris)
#TWELVE-E###
###F########
###ITWO-N###
###V########
###E########
###-FIVE-R##
###SFOUR-W##
>>> print(inventaris.plaats('L', 2, 'V1:10').plaats('U', 3, 'V1:11').plaats('H', 3, 'V1:12'))
#TWELVE-ETTT
###F#####WHH
###ITWO-NORR
###V#####-EE
###E#####LEE
###-FIVE-R--
###SFOUR-WUH
>>> print(inventaris.plaats('V', 6, 'H2:5').plaats('F', 6, 'H4:5').plaats('T', 6, 'H5:5'))
#TWELVE-ETTT
###FSIX-VWHH
###ITWO-NORR
###VSIX-F-EE
###ESIX-TLEE
###-FIVE-R--
###SFOUR-WUH
>>> inventaris.volledig()
False
>>> print(inventaris.plaats('I', 7, 'V1:1').plaats('O', 5, 'V2:2').plaats('X', 4, 'V2:3'))
STWELVE-ETTT
EFFFSIX-VWHH
VIOITWO-NORR
EVUVSIX-F-EE
NERESIX-TLEE
----FIVE-R--
IOXSFOUR-WUH
>>> inventaris.volledig()
True
>>> inventaris.opgelijste_voorkomens()
{'E': 12, 'F': 6, 'H': 3, 'I': 7, 'L': 2, 'N': 2, 'O': 5, 'R': 5, 'S': 5, 'T': 6, 'U': 3, 'V': 6, 'W': 4, 'X': 4}
>>> inventaris.waargenomen_voorkomens()
{'E': 12, 'F': 6, 'H': 3, 'I': 7, 'L': 2, 'N': 2, 'O': 5, 'R': 5, 'S': 5, 'T': 6, 'U': 3, 'V': 6, 'W': 4, 'X': 4}
>>> inventaris.zelfbeschrijvend()
True