Onderstaande reeks is één van de eerste oneindige reeksen die bepaald werd in de geschiedenis van de wiskunde. De Griekse wiskundige Archimedes bepaalde de som hiervan reeds in 200 voor Christus.
\[\dfrac{1}{3} = \sum_{n=1}^\infty \dfrac{1}{4^n}\]Er bestaat een ontroerend mooi meetkundig argument voor deze reekssom. In onderstaand vierkant stelt het oranje deel deze oneindige som voor, eerst één vierde, daarna één zestiende, enz… De groene en blauwe oppervlaktes werden echter net op dezelfde manier opgebouwd. Alles samen krijg je dus de oppervlakte van het volledige vierkant. Dat betekent dat één kleur één derde van het volledige vierkant vormt.
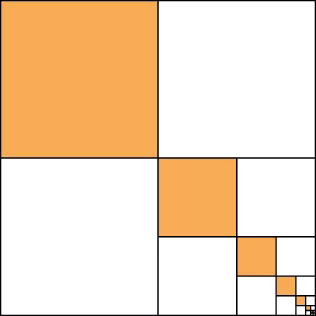

Gevraagd
- Maak een functie
archimedes(aantal)waarbijaantalhet aantal termen uit de som voorstelt. Zo geldt datarchimedes(3)overeenkomt met
- Laat R het resultaat van de som afronden op 9 cijfers na de komma.
Voorbeelden
De eerste 3 termen van de som optellen resulteert in:
> archimedes(3)
[1] 0.328125
De eerste 10 termen van de som optellen resulteert in:
> archimedes(10)
[1] 0.333333