Een standaard kaartspel bestaat uit 52 Franse speelkaarten. Zoals aangegeven in onderstaande tabel zijn ze onderverdeeld in 13 rangen (kolommen) voor elk van de 4 kleuren (rijen): klaveren (♣, clubs), koeken (♦, diamonds), harten (♥, hearts) en schoppen (♠, spades). In de tabel zijn de rangen van links naar rechts geordend volgens stijgende waarde.
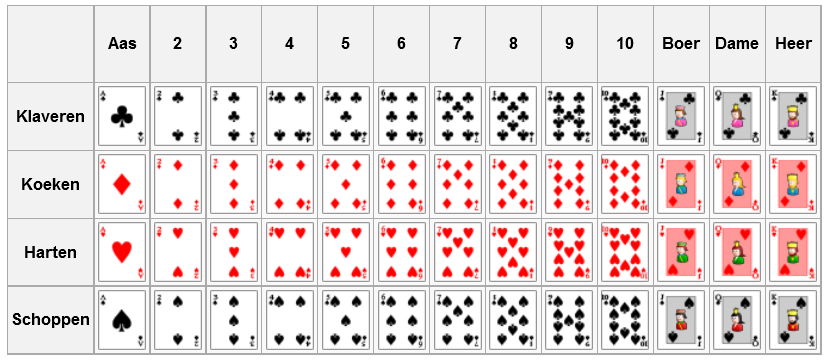
Een speelkaart wordt genoteerd als twee karakters die respectievelijk de rang en de kleur van de kaart aanduiden. Kleuren worden aangeduid met kleine letters, namelijk de eerste letter van de Engelse benaming voor de kleur (c, d, h en s). Rangen worden in oplopende volgorde aangeduid als A (aas), de cijfers 2 tot en met 9, T (tien), J (boer, jack), Q (dame, queen) en K (heer, king). Klaveren aas wordt dan bijvoorbeeld voorgesteld als Ac. De boer, dame of heer worden voorgesteld als symmetrische prentkaarten die niet van uitzicht veranderen als je ze ondersteboven bekijkt.
In deze opgave bestaat een hand uit 13 verschillende kaarten die willekeurig gekozen werden uit een spel van 52 kaarten. Een hand kan dus voorgesteld worden door 26 karakters, wat meteen ook een volgorde oplegt aan de kaarten in een hand.
Opgave
Elke regel van het tekstbestand cards.txt bevat 26 karakters die een hand kaarten voorstellen, gevolgd door één enkele spatie en een woord dat enkel uit letters bestaat. Gevraagd wordt:
-
Bepaal reguliere expressies voor elk van onderstaande verzamelingen. Daarbij staat $$\mathcal{H}$$ voor de verzameling van alle voorstellingen van handen als een reeks van 26 karakters. Probeer de reguliere expressies bovendien zo kort mogelijk te houden.
-
$$\alpha = \{ h \in \mathcal{H}\,|\,$$ $$h$$ bevat geen prentkaarten$$\}$$
voorbeelden: 2s4d5h7cTs6hTh6c5s9d2cTd9s $$\in \alpha$$Ah9cJd7d8c5d9hTsAcQc5s4cTc $$\not\in \alpha$$ -
$$\beta = \{ h \in \mathcal{H}\,|\,$$ $$h$$ bevat de vier kaarten van eenzelfde rang$$\}$$
voorbeelden: Kd9dJs5sKs7c5c6cKcJhKhTh7h $$\in \beta$$AdTdTc2d2cTsKh6c3c6s6dKc4h $$\not\in \beta$$ -
$$\gamma = \{ h \in \mathcal{H}\,|\,$$ $$h$$ bevat minstens drie kaarten van elke kleur$$\}$$
voorbeelden: Ad7hTc4h8d8sAsQhJdTs $$\in \gamma$$5dKc9cJcTh7sQc3s4sAs7c2cTs $$\not\in \gamma$$ -
$$\delta = \{ h \in \mathcal{H}\,|\,$$ de kaarten van $$h$$ zijn gegroepeerd per kleur$$\}$$ (tussen twee kaarten van eenzelfde kleur staan nooit kaarten van een andere kleur)
voorbeelden: 9s5s4sKs7h6h4h2d4dAdTd2c3c $$\in \delta$$5s9sTs8hKhJc4s6c4hJsAc2dKs $$\not\in \delta$$
Gebruik een commando uit de grep familie om enkel die regels van het bestand cards.txt te selecteren die behoren tot de opgegeven verzameling.
-
-
Beschouw de verzamelingen $$\alpha$$, $$\beta$$, $$\gamma$$ en $$\delta$$ zoals hierboven gedefinieerd. Gebruik nu deze verzamelingen om op de volgende manier een boodschap bestaande uit vier woorden te achterhalen:
-
Het eerste woord staat op de unieke regel met het patroon uit de verzameling $$\alpha \cap \beta$$
-
Het tweede woord staat op de unieke regel met het patroon uit de verzameling $$\beta \cap \gamma$$
-
Het derde woord staat op de unieke regel met het patroon uit de verzameling $$\gamma \cap \delta$$
-
Het vierde woord staat op de unieke regel met het patroon uit de verzameling $$\delta \cap \alpha$$
Geef telkens een Unix commando dat elk van deze woorden opzoekt in het bestand en uitschrijft naar standaard uitvoer (zonder het patroon dat aan het woord voorafgaat). Hierbij is het dus niet toegelaten om het woord letterlijk uit te schrijven (bv. echo xxx).
-