A billboard is divided into vertical strips that are all of the same width. A series of posters are successively attached to the board. The posters have the same height as the billboard itself, are attached at different positions on the billboard, and thereby exactly cover a sequence of strips. However, the poster are not all of the same width, and are possibly stuck on top of each other. How many posters will finally be (partially) visible.

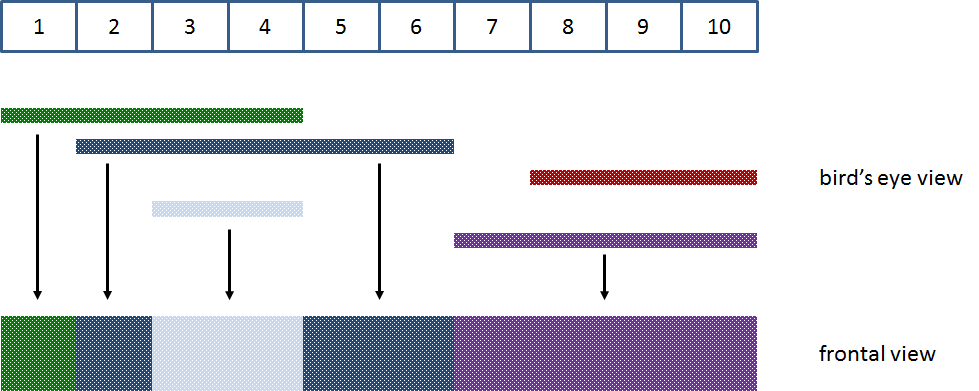
As an example, suppose that a billboard has ten strips and five posters are attached to it in the following order:

• a poster that starts at strip 1 and is 4 strips wide

• a poster that starts at strip 2 and is 5 strips wide

• a poster that starts at strip 8 and is 3 strips wide

• a poster that starts at strip 3 and is 2 strips wide

• a poster that starts at strip 7 and is 4 strips wide

A graphical representation of this situation as given below, clearly shows that in the end four out of five posters are (partially) visible.

Note that you should not make the assumption that billboards are always subdivided into ten strips, as is the case in the above example.

Assignment

Write a function visible that takes a list of tuples, where each tuple contains two integers. The tuples describe the positions and the order of a sequence of posters that are attached on a billboard. The first tuple corresponds to the poster that is attached first. The last tuple with the poster that is attached at the end. The first integer of a tuple gives the index of the strip that is covered by the left part of the poster, and the second integer indicates the number of strips covered by the poster. The function should return how many posters are eventually (partially) visible.

Example

>>> visible([(1, 4), (2, 5), (8, 3), (3, 2), (7, 4)])
4
>>> visible([(3, 5), (1, 4), (5, 6)])
2
>>> visible([(2, 1), (5, 1)])
2