Find the errors

There is already some code, but there are still errors. Correct all the errors and submit to get feedback.

A quadratic equation is any equation that can be rearranged in standard form as

\[ax^2 + bx + c = 0\]

, where \(a, b, c \in \mathbb{R}\) and \(a \neq 0\).

The expression

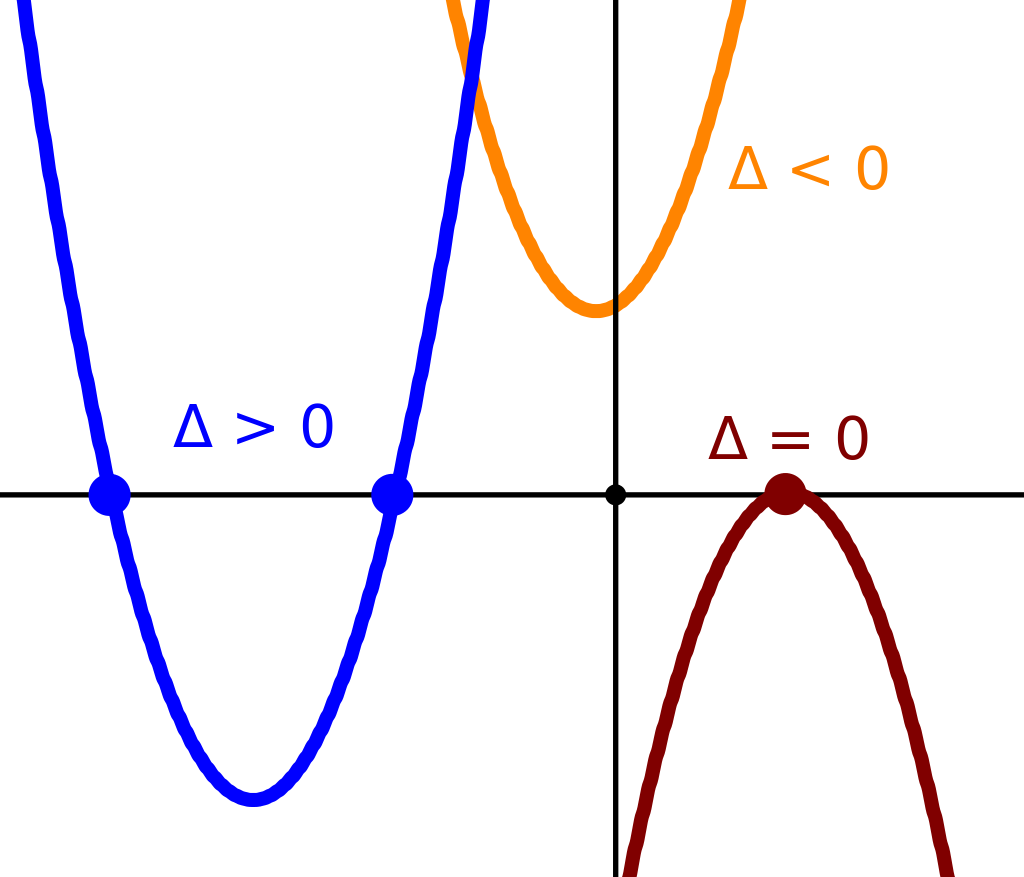
\[\Delta = b^2 - 4ac\]

is called the discriminant of the quadratic equation. The sign of \(\Delta\) determines the number of real-valued solutions. If \(\Delta > 0\), then there are two distinct real-valued solutions (\(x_1 \neq x_2\)). The real-valued solutions can be determined as:

\[x_{1} = \frac{-b - \sqrt{\Delta}}{2a}\ \ \ \text{en}\ \ \ x_{2} = \frac{-b + \sqrt{\Delta}}{2a}\]

Input

The three parameters \(a\), \(b\) and \(c\) of a quadratic equation, each on a separate line.

Output

You may assume that in this exercise it is always a valid quadratic equation with two solutions each time (discriminant is always greater than 0, \(\Delta > 0\)), which must be printed. Always state \(x_1\) first and \(x_2\) on the next line.

Example 1

The zero points of \(1x^2 + 4x -5\) are \(x_1 = -5\) and \(x_2 = 1.0\).

Input:

1
4
-5

Output:

Zero point 1: -5.0
Zero point 2: 1.0

Example 2

The zero points of \(2x^2 + 5x -3\) are \(x_1 = -3\) and \(x_2 = -0.5\).

Input:

2
5
-3

Output:

Zero point 1: -3.0
Zero point 2: 0.5