Speleology is a sub-domain of the geosciences that deals with the study of caves. Although considered serious science, the exploration of underground cavities also encompasses certain elements of sportiness, adventure and courage. Exploring caves, especially if their structure is only partially known, is not without any danger and requires skill and training.

Speleology is a cross-disciplinary field that combines knowledge of chemistry, biology, geology, physics, meteorology and cartography to develop portraits of caves as complex, evolving systems. It is the scientific study of the make-up of caves and other karst features, their structure, physical properties, history, life forms, and the processes by which they form (speleogenesis) and change over time (speleomorphology). The term speleology is also sometimes applied to the recreational activity of exploring caves, but this is more properly known as caving, spelunking or potholing. Speleology and caving are often connected, as the physical skills required for in situ study are the same.

Assignment

As part of your speleology training, you are given the map of a cave that consists of a number of halls. The halls of the cave are arranged in a rectangular $$m \times n$$ grid with $$m$$ rows and $$n$$ columns. The cave has only a single entrance and a single exit which are located in a hall at the edge of the grid. Each hall is connected to each of its neighbouring halls north, south, east and west, unless it collides with the edge of the cave. Your task is to find a valid path that goes from the hall where the entrance of the cave is located, and winds its way by visiting neighbouring halls until the hall is reached where the exit is located. The path may not go through any hall more than once. In addition, the cave map contains clues that tell how many halls the path passes in each row and column of the grid.

A sample map of a cave whose halls are arranged in a $$5 \times 5$$ grid is given below. In order to reference the halls in the grid, we increasingly index the rows from north to south and the columns from west to east, with indexing starting at zero (grey numbers on the sample map). The cave has an entrance at the western edge of hall (0, 0) and an exit at the eastern edge of hall (3, 4). A path is described as a succession of letters that indicate which of the neighbouring halls is visited next: N (north), S (south), E (east) or W (west).

Map of a cave that has its halls arranged in 5 rows and 5 columns, with an entrance in hall (0, 0) and an exit in hall (3, 4). The path ESWSSEENESE (center) leads to the exit, with the number of passages through the rows and the columns of the map indicated in green. The path EESSWW (left) does not lead to the exit. The path EESWWW (right) collides with the western edge of the cave.

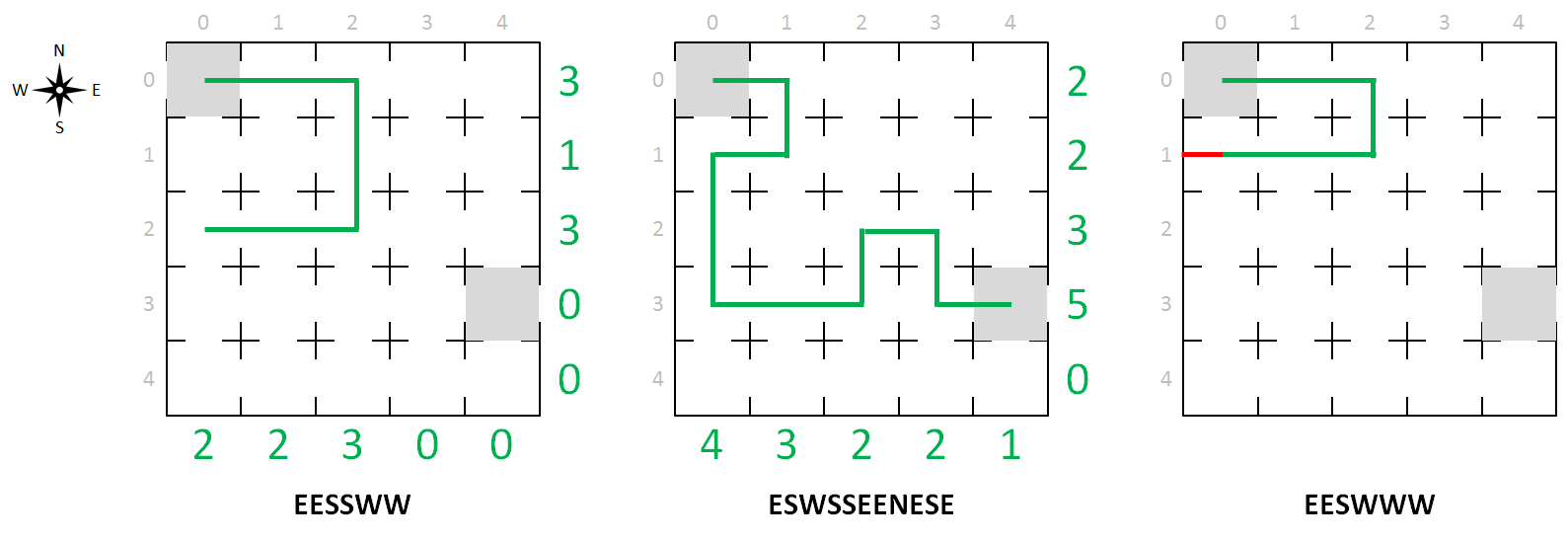
The path ESWSSEENESE (center map in the figure) winds its way from the entrance to the exit, with the number of passages through the rows and columns of the map indicated in green. As such, there are for example 2 passages through the northernmost row and 4 passages through the westernmost column. In addition, the path visits each hall in the grid at most once. The path EESSWW (left map) is invalid because it does not lead the the exit. The path EESWWW (right) is equally invalid because it collides with the western edge of the cave.

Your task is to implement a class Cave whose objects represent a cave map. The cave consists of a number of halls, arranged in a rectangular $$m \times n$$ grid. Apart from the positions of the entrance and the exit of the cave, the map also contains clues that tell how many halls a valid path passes through each row and column of the grid. Make sure the objects of the class at least support the following methods, which can be used to check whether or not a given path is valid.

An initialization method that can be used to define a cave map and the expected number of passages through each row and column of the grid. The method takes four arguments that are all sequences (lists or tuples) of positive integers. The first argument contains $$m$$ integers that indicate how many halls a valid path visits in each row (from north to south) of the grid. The second argument contains $$n$$ integers that indicate how many halls a valid path visits in each column (from west to east) of the grid. The last two arguments contain the row index $$r$$ and the column index $$c$$ of the halls where respectively the entrance and the exit of the cave are located. The initialization method must raise an AssertionError with the message invalid cave map, in case at least one of the following conditions is not met:

all integers in the first argument are in the interval $$[0, n]$$
all integers in the second argument are in the interval $$[0, m]$$
the halls where the entrance and exit of the cave are located are at the edge of the grid

A method path that takes a string argument. The given string must contain a sequence of the letters N (north), S (south), E (east) and W (west). These letters describe the successive movements to neighbouring halls that are followed by a path, starting from the hall where the entrance of the cave is located. The method must return a list containing the positions of the halls in the order in which they are visited by the given path. The position of a hall is described by a tuple $$(r, c)$$, where $$r$$ indicates the row index and $$c$$ the column index of the hall in the grid. In case the given path would make a movement that forces it to collide with the edge of the cave, the method must raise an AssertionError with the message collides with cave.
A method passages that takes a string argument that has the same meaning as the argument passed to the method path. In case this string describes a path starting from the entrance that would make a movement that forces it to collide with the edge of the cave, the method must raise an AssertionError with the message collides with cave. The method must return a tuple that itself contains two tuples, respectively containing the number of halls visited by the given path in each row (from north to south) and column (from west to east) of the grid.
A method validPath that takes a string argument that has the same meaning as the argument passed to the method path. In case this string describes a path starting from the entrance that would make a movement that forces it to collide with the edge of the cave, the method must raise an AssertionError with the message collides with cave. The method must return a Boolean value that indicates whether or not the given path is valid. A path is valid if it i) ends in the hall where the exit of the cave is located, ii) does not visit the same hall more than once, iii) passes through each row the expected number of times and iv) passes through each column the expected number of times.

Example

>>> cave = Cave((2, 2, 3, 5, 0), (4, 3, 2, 2, 1), (0, 0), (3, 4))

>>> cave.path('EESSWW')
[(0, 0), (0, 1), (0, 2), (1, 2), (2, 2), (2, 1), (2, 0)]
>>> cave.passages('EESSWW')
((3, 1, 3, 0, 0), (2, 2, 3, 0, 0))
>>> cave.validPath('EESSWW')
False

>>> cave.path('ESWSSEENESE')
[(0, 0), (0, 1), (1, 1), (1, 0), (2, 0), (3, 0), (3, 1), (3, 2), (2, 2), (2, 3), (3, 3), (3, 4)]
>>> cave.passages('ESWSSEENESE')
((2, 2, 3, 5, 0), (4, 3, 2, 2, 1))
>>> cave.validPath('ESWSSEENESE')
True

>>> cave.path('EESWWW')
Traceback (most recent call last):
AssertionError: collides with edge
>>> cave.passages('EESWWW')
Traceback (most recent call last):
AssertionError: collides with edge
>>> cave.validPath('EESWWW')
Traceback (most recent call last):
AssertionError: collides with edge

>>> cave = Cave((2, 2, 3, 6, 0), (4, 3, 2, 2, 1), (0, 0), (3, 4))
Traceback (most recent call last):
AssertionError: invalid cave map

>>> cave = Cave((2, 2, 3, 5, 0), (4, 3, 2, 2, 1), (1, 1), (3, 4))
Traceback (most recent call last):
AssertionError: invalid cave map