Zwart Gat is een spel voor twee spelers. Het wordt gespeeld op een spelbord met 36 zeshoekige tegels die in de vorm van een driehoek geschikt worden. Aan het begin van het spel zijn deze tegels leeg, op vijf bruine stenen na die op willekeurig gekozen plaatsen op het spelbord gelegd worden.

Mogelijke configuratie van het spelbord bij aanvang van een spelletje Zwart Gat.

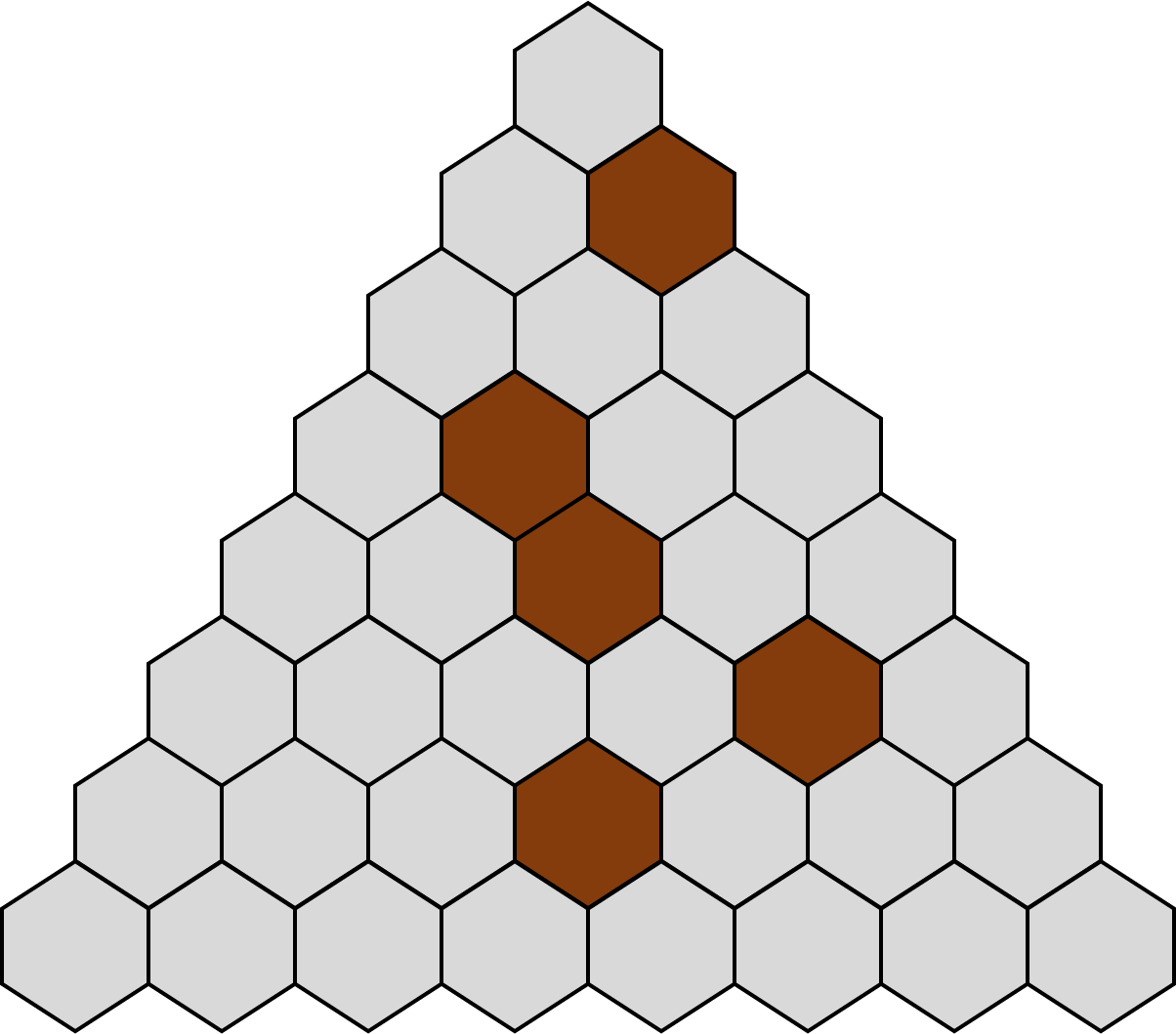
Spelverloop

Bij aanvang van het spel hebben beide spelers elk 15 stenen van hun kleur — rood of blauw — die gemarkeerd zijn met de getallen 1 tot en met 15. De spelers plaatsen om beurt één van hun stenen die ze nog niet geplaatst hebben op een vrije tegel: tegels waarop reeds een bruine, rode of blauwe steen geplaatst werd zijn niet meer vrij. De speler met de rode stenen begint, en het spel is dus afgelopen na in totaal 30 beurten.

Als gevolg van deze regels is er op het einde van het spel één lege tegel over. Er zijn immers 36 tegels en slechts 35 stenen: 5 bruine stenen, 15 blauwe stenen en 15 rode stenen. De tegel die leeg blijft, wordt het zwart gat genoemd. Omdat het een zwart gat is, worden alle aangrenzende tegels in dit gat gezogen.

Score

Wie het spel wint, hangt af van het aantal punten die in het zwart gat terechtkomen. Als $$r$$ het aantal punten is op de rode stenen die aan het zwart gat grenzen, en $$b$$ is het aantal punten op de blauwe stenen die aan het zwart gat grenzen, dan krijgt de rode speler $$75 + r - b$$ punten en de blauwe speler $$75 + b - r$$ punten. Kijk bij wijze van voorbeeld eens naar de volgende eindconfiguratie van het spelbord:

Mogelijke configuratie van het spelbord op het einde van een spelletje Zwart Gat.

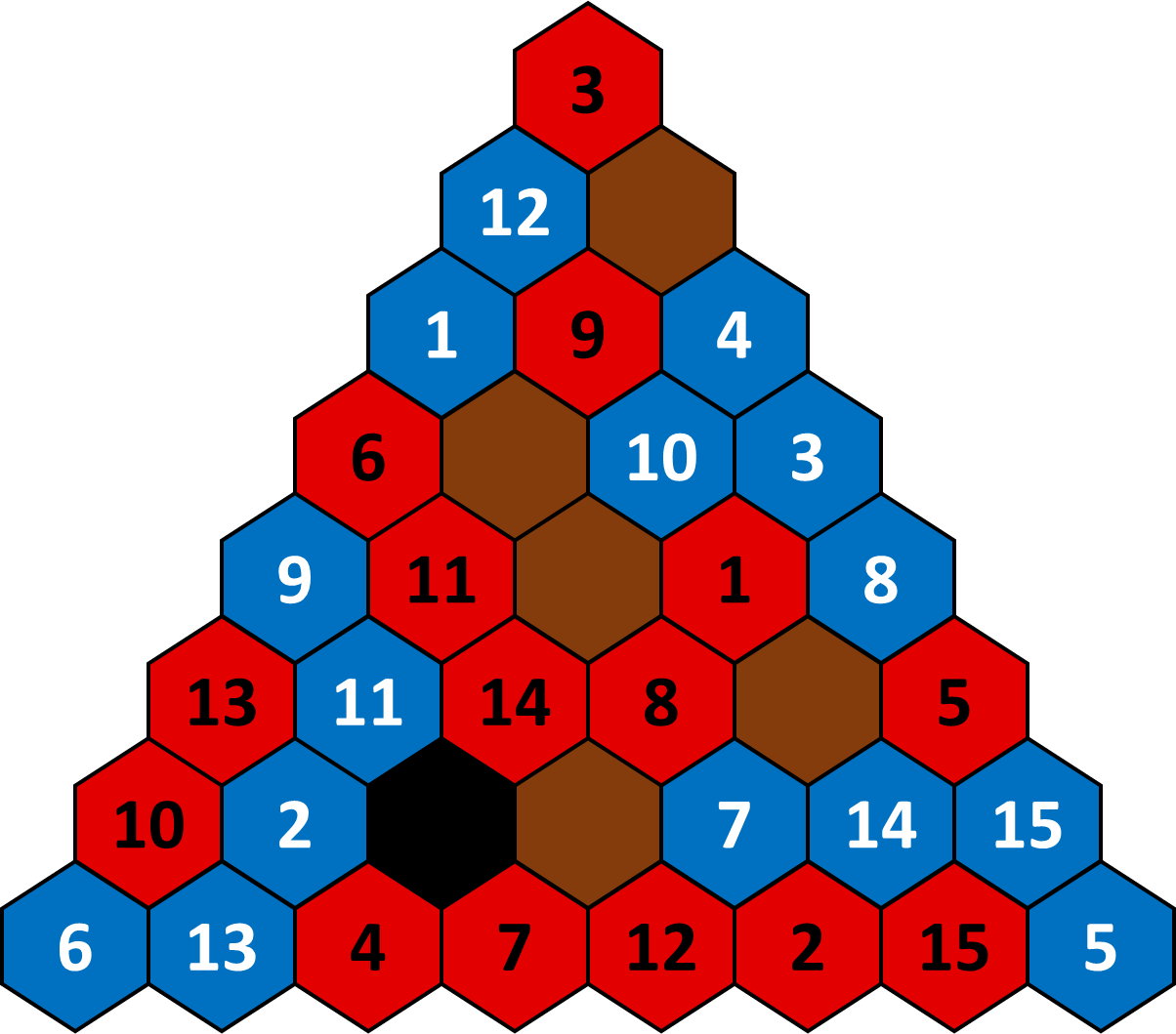
Rood heeft drie stenen rondom het zwart gat (dat in de afbeelding ook in het zwart wordt aangegeven). Deze stenen hebben de waarden 4, 7 en 14, en dus krijgen we dat $$r = 4 + 7 + 14 = 25$$. Blauw heeft twee stenen met waarden 2 en 11 rondom het zwart gat, en dus krijgen we dat $$b = 2 + 11 = 13$$. Rood verdient aan dit spel dus $$75 + 25 - 13 = 87$$ punten en blauw verdient $$75 + 13 - 25 = 63$$ punten.

Opgave

In deze opgave moet je op basis van een gegeven eindconfiguratie van een spelletje Zwart Gat bepalen hoeveel punten de rode en de blauwe speler verdienen. De eindconfiguratie wordt omschreven in een tekstbestand dat bestaat uit 8 regels. De $$i$$-de regel ($$i = 1, 2, \ldots, 8$$) bevat de omschrijving van de $$i$$ stenen (van links naar rechts) op de $$i$$-de rij van het spelbord (van boven naar onder), telkens van elkaar gescheiden door één enkele spatie. De verschillende stenen worden op de volgende manier omschreven:

het zwart gat wordt omschreven door de hoofdletter X
bruine stenen worden omschreven door een asterisk (*)
blauwe stenen worden omschreven door de waarde van de steen, gevolgd door de hoofdletter B
rode stenen worden omschreven door de waarde van de steen, gevolgd door de hoofdletter R

Hieronder zie je bijvoorbeeld de omschrijving van de eindconfiguratie die overeenkomt met de grafische voorstelling van de eindconfiguratie uit de inleiding van deze opgave.

3R
12B *
1B 9R 4B
6R * 10B 3B
9B 11R * 1R 8B
13R 11B 14R 8R * 5R
10R 2B X * 7B 14B 15B
6B 13B 4R 7R 12R 2R 15R 5B

Gevraagd wordt om een klasse ZwartGat te definiëren die kan gebruikt worden om de score te berekenen op basis van een gegeven eindconfiguratie van het spelletje Zwart Gat. Deze klasse moet minstens de volgende methoden ondersteunen:

Een initialisatiemethode waaraan de locatie van een tekstbestand moet doorgegeven worden. Dit bestand moet een geldige omschrijving van de eindconfiguratie van een spelletje Zwart Gat bevatten. Indien het bestand geen omschrijving van een eindconfiguratie bevat conform de spelregels van het spelletje Zwart Gat en conform de opmaak zoals hierboven beschreven, dan moet een AssertionError opgeworpen worden met de boodschap ongeldig spelbord.
Een methode score waaraan geen argumenten moeten doorgegeven worden. Deze methode moet een tuple teruggeven met daarin twee gehele getallen die respectievelijk de score van rood en blauw aangeven op basis van de gegeven eindconfiguratie van het spelletje Zwart Gat.

Voorbeeld

Bij onderstaande voorbeeldsessie gaan we ervan uit dat de tekstbestanden geldig_spelbord.txt¹ en ongeldig_spelbord.txt² zich in de huidige directory bevinden.

        >>> spelbord = ZwartGat('geldig_spelbord.txt')
>>> spelbord.score()
(87, 63)

>>> ZwartGat('ongeldig_spelbord.txt')
Traceback (most recent call last):
AssertionError: ongeldig spelbord

Opgave

Voorbeeld

Epiloog