Er zijn twee manieren om een punt in een vlak voor te stellen: cartesische coördinaten en poolcoördinaten. In het eerste coördinatensysteem wordt elk punt voorgesteld door een \(x\)- en een \(y\)-coördinaat. In het tweede coördinatensysteem wordt elk punt voorgesteld door een straal \(r\) (de afstand tot de oorsprong) en een hoek \(\theta\). Deze hoek wordt uitgedrukt in radialen, en er moet gelden dat \(−\pi<\theta≤\pi\).
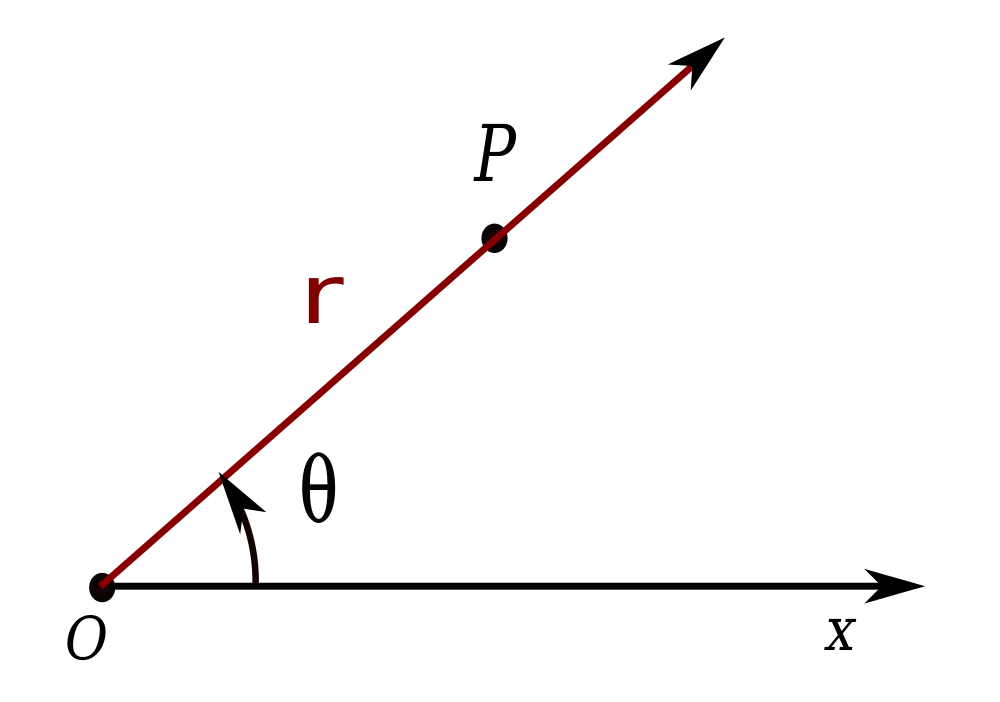
Het verband tussen de carthesische coördinaten \((x,y)\) en de poolcoördinaten \((r,\theta)\) wordt dan gegeven door:
\[\begin{cases} r = & \sqrt{x^2+y^2} \\ \\ \theta = & \arctan\left(\frac{y}{x}\right) \end{cases}\]Opgave
Schrijf een functie poolcoordinaten waaraan één tuple \((x,y)\) met twee reële getallen als enige parameter wordt meegegeven. De functie geeft het tuple \((r, hoek)\) terug, met de overeenkomstige poolcoördinaten.
Tip: gebruik atan2 voor het berekenen van de hoek. Bekijk eventueel de oefening uit de eerste reeks (je mag de oplossing gebruiken).
Voorbeelden
>>> poolcoordinaten((137, 0))
(137.0, 0.0)
>>> poolcoordinaten((0, 166.3))
(166.3, 1.5707963267948966)
>>> poolcoordinaten((-30.0, 22.0))
(37.20215047547655, 2.5088438185876103)