Preparation

The module random¹ from the Standard Python Library can be used for (amongst other things) generating random numbers. The function random() from this module generates a random real number from the interval $$[0, 1[$$. The function randint(a, b) on the other hand, can be used to generate a random integer from the interval $$[a, b]$$. The interactive Python session below indicates how you can use the functions from the random module with some examples.

>>> import random
>>> help(random.random)
Help on built-in function random:

random(...)
    random() -> x in the interval [0, 1).
>>> random.random()
0.954131645221452
>>> random.random()
0.3548429482674793

>>> help(random.randint)
Help on method randint in module random:

randint(self, a, b) method of random.Random instance
    Return random integer in range [a, b], including both end points.
>>> random.randint(3, 10)
5
>>> random.randint(3, 10)
8

Description

A sphere can be represented as a collection of all points on a distance $$r$$ from the central point $$(0,0,0)$$. If $$r=1$$, it is named a unit sphere. The Marsaglia method² can be used to generate a random point on a sphere with radius $$r$$. In a first step of this method, a random point $$(x_1,y_1)$$ is chosen that lays within the unit sphere. To this point applies that: $$x_1^2+y_1^2\leq 1$$. In order to do this, random points are generated in the 2-by-2 square $$[-1,1]\times[-1,1]$$ with centre in $$(0,0)$$, until a point is found that lays within the unit sphere. 

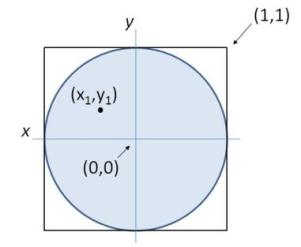
The point $$(x_1,y_1)$$ is used in the following way to determine the $$(x,y,z)$$ co-ordinates of a random point on a circle with radius $$r$$: \[ \begin{aligned} x & = 2 r x_1 \sqrt{1 - x_1^2 - y_1^2} \\ y & = 2 r y_1 \sqrt{1 - x_1^2 - y_1^2} \\ z & = r - 2r(x_1^2 + y_1^2) \end{aligned} \]

Assignment

Write a function that can be used to generate a random point on a sphere with radius $$r \in \mathbb{R}$$. A value for $$r$$ can be given to the function optionally. Standard, the random point is generated on the unit sphere. The function must print a tuple with the $$(x,y,z)$$ co-ordinates of the random point.

Example

>>> spherecoordinate()
(0.8208783192500947, 0.24904502507471912, 0.5139410087458212)
>>> spherecoordinate()
(0.1705946803883025, 0.9853183076681309, 0.006729606022916168)
>>> spherecoordinate()
(0.5245775493577824, 0.47160784998323607, -0.7088049312356488)

>>> spherecoordinate(1.2)
(1.006669684101887, 0.41835600224171376, 0.10767730725894864)
>>> spherecoordinate(5.8)
(0.3653448756504214, 0.8635619785170504, -2.2182839834195476)
>>> spherecoordinate(4.9)
(0.5245775493577824, 0.47160784998323607, -0.7088049312356488)