A Hertzsprung-Russell diagram is a scatter graph. The vertical axis shows the brightness of a star, expressed as absolute magnitude (magnitude corrected for distance and interstellar obscuration) or relative light intensity towards the sun. The horizontal axis shows a variable related to surface temperature, such as the B-V color index, the spectral type, or the actual temperature. Note: the temperature increases from right to left. The diagram is the usual base for the classification of stars and is used to describe their evolution. It was named after Ejnar Hertzsprung and Henry Norris Russell who introduced it independently around 1910.

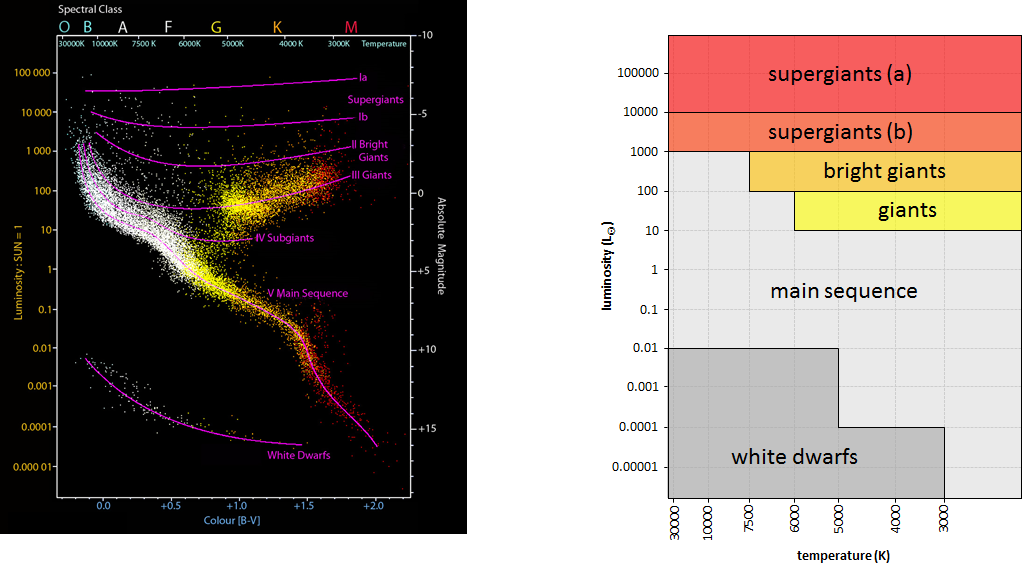
Based on the position of the stars within a Hertzsprung-Russell diagram, the following classes are distinguished: supergiants (a), supergiants (b), bright giants, giants, the main sequence and white dwarfs. There is no univocal distinguishing of the areas within the diagram that correspond with the classes. For this assignment, we will take the picture on the right as a starting point. De borders of every area are parallel with one of the axis of the diagram and always correspond with one of the figures on the axis.

Assignment

• Write a function classification to which two floating point numbers must be passed that respectively represent the temperature (in Kelvin) and the luminosity (relative to the sun) of a star. The function should return a string that indicates the class of the star, according to the classification in the above figure on the right. You may assume that the values of the temperature and the luminosity are alwayrs within the limits of the image, and that they will never form a point that is situated on a border of the areas used for dividing.

• Write a function catalogue to which the location of a text file must be passed. The file describes a number of stars. The firs line contains a header. The following lines each contain information about one single star in fields that are separates by one tab: i) name) , ii) stellar classification, iii) temperature (in Kelvin), iv) luminosity, v) mass and vi) radius. The last three information fields are each time expressed relative to the sun. The function must return a dictionary, that displays the name of each star on a tuple that contains the floating point values of the temperature and luminosity of the star.

• Write a function classes to which a dictionary must be passed that is built like the dictionaries returned by the function catalogue. The function should return a new dictionary, that displays the name of a class of stars on the collection of names of stars from the given dictionary that belong to this class. The name of a class of stars can only be used as a key in this new dictionary, if the given dictionary also contains stars that belong to this class.

Example

In the following example session we assume that the text file stars.txt¹ is in the current directory.

>>> classification(8525.0, 196000.0) # Deneb
'supergiants (a)'
>>> classification(18890.0, 3300.0)  # Sigma Sagittarii
'supergiants (b)'
>>> classification(4925.0, 132.0)    # Zeta Hydrae
'bright giants'
>>> classification(4810.0, 45.0)     # Delta Arietis
'giants'
>>> classification(13397.0, 148.0)   # Zeta Draconis
'main sequence'
>>> classification(7740.0, 0.00049)  # Procyon A
'white dwarfs'

>>> stars = catalogue('stars.txt')
>>> stars
{'Beta Herculis': (4887.0, 151.0), 'Omicron Ursae Majoris': (5242.0, 138.0), 'Alpha Columbae': (12963.0, 1000.0), 'Beta Ursae Minoris': (4030.0, 390.0), 'Zeta Aquilae': (9620.0, 39.4), 'Epsilon Sagittarii': (5807.0, 0.89), 'Nu Ophiuchi': (4928.0, 123.0), 'Pi Orionis': (6516.0, 2.822), 'Beta Lyrae': (13300.0, 6.5), 'Beta Ceti': (4797.0, 139.1)}

>>> classes(stars)
{'main sequence': {'Pi Orionis', 'Alpha Columbae', 'Epsilon Sagittarii', 'Zeta Aquilae', 'Beta Lyrae'}, 'bright giants': {'Beta Herculis', 'Omicron Ursae Majoris', 'Nu Ophiuchi', 'Beta Ceti', 'Beta Ursae Minoris'}}