Protein folding is the physical process by which a protein¹ folds in an expeditious and reproducible manner into its native² three-dimensional structure³, a conformation⁴ that is usually biologically functional. Each protein exists as an unfolded polypeptide⁵ that lacks any stable structure when translated⁶ from a sequence of mRNA⁷ to a linear chain of amino acids⁸ (figure: left). As the polypeptide chain is being synthesized by a ribosome⁹, the linear chain begins to fold into its three-dimensional structure (figure: right).

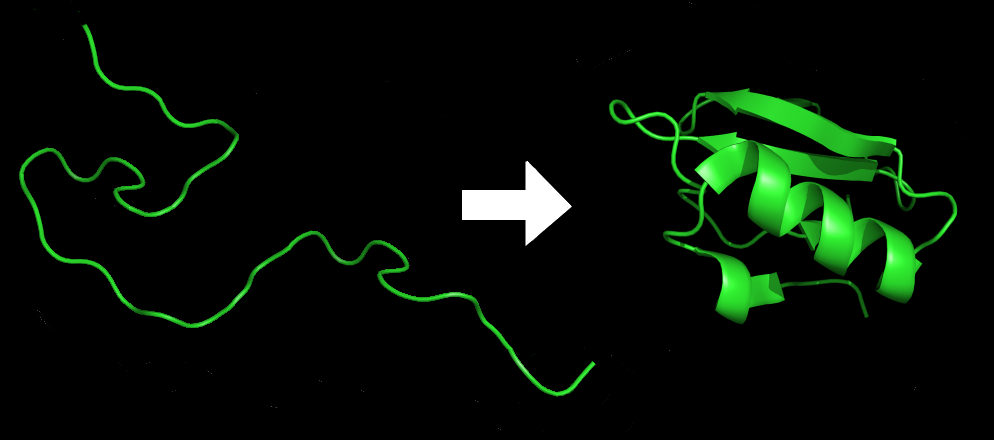
The resulting three-dimensional structure is determined completely by the amino acid sequence (Anfinsen's dogma¹⁰), called the primary structure. Understanding and simulating the protein folding process has been an important challenge for computational biology¹¹ since the late 1960s.

The hydrophobic-polar (HP) model is a highly simplified model for examining protein folds in space. First proposed by Ken Dill in 1985, it is the best-known grid model for protein folding. It stems from the observation that hydrophobic interactions between amino acid residues are the driving force for protein folding. All amino acids are classified as either hydrophobic (H) or polar (P), and the fold of a protein sequence is defined as a self-avoiding walk in a two-dimensional or three-dimensional grid. The HP model imitates the hydrophobic effect by assigning a negative weight to interactions between adjacent hydrophobic amino acids and looking for folds that yield minimum energy.

Assignment

The primary structure of a protein is represented as a sequence (str) of hydrophobic (H) and polar (P) amino acids, e.g. HHPPHHHPHHPH. The order of the amino acids is important: HPP and PPH are distinct proteins.

In nature, proteins are folded into three-dimensional structures, but for simplicity we'll look at protein folding in two dimensions. In the HP model, the amino acids of a folded protein occupy the cells of a grid: at most one amino acid per cell. Proteins are folded in such a way that the number of H-H contact points is as large as possible, because this is energetically advantageous. The figures below show two possible ways in which the same protein can be folded. The blue cell indicates the position of the first amino acid in the protein sequence. The green line indicates the order of the amino acids in the protein sequence. The red dots indicate the H-H contact points.

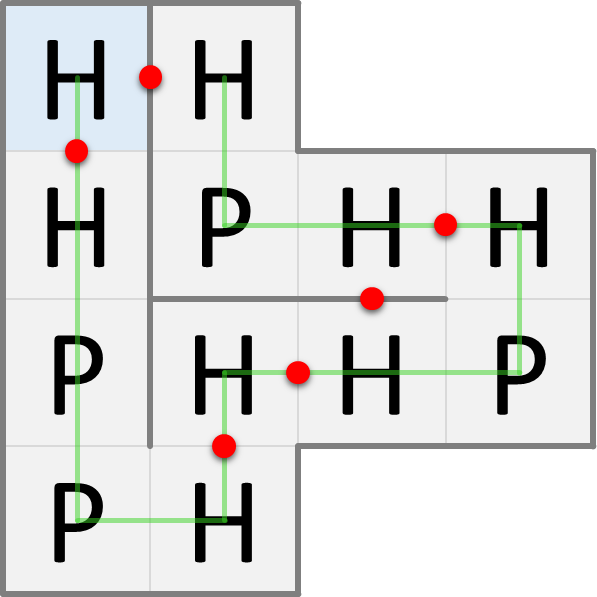
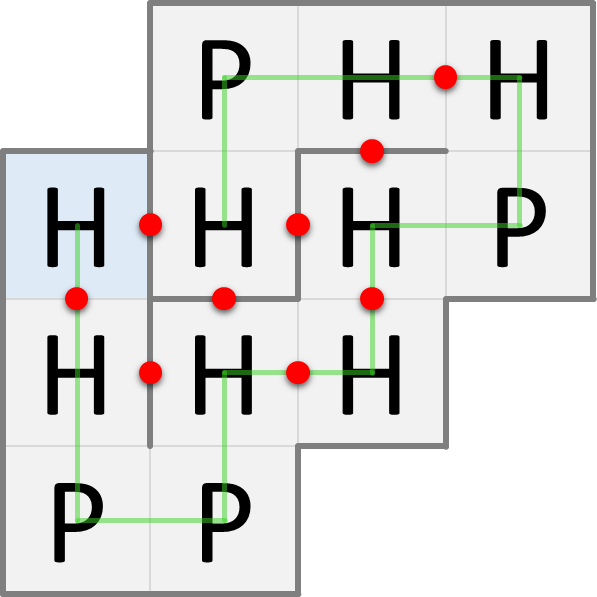
The fold on the left has only 6 H-H contact points, whereas the fold on the right has 9 H-H contact points. The maximum number of H-H contact points that can be obtained for this protein is 9, so the fold on the right is the one that will occur naturally according to the HP model.

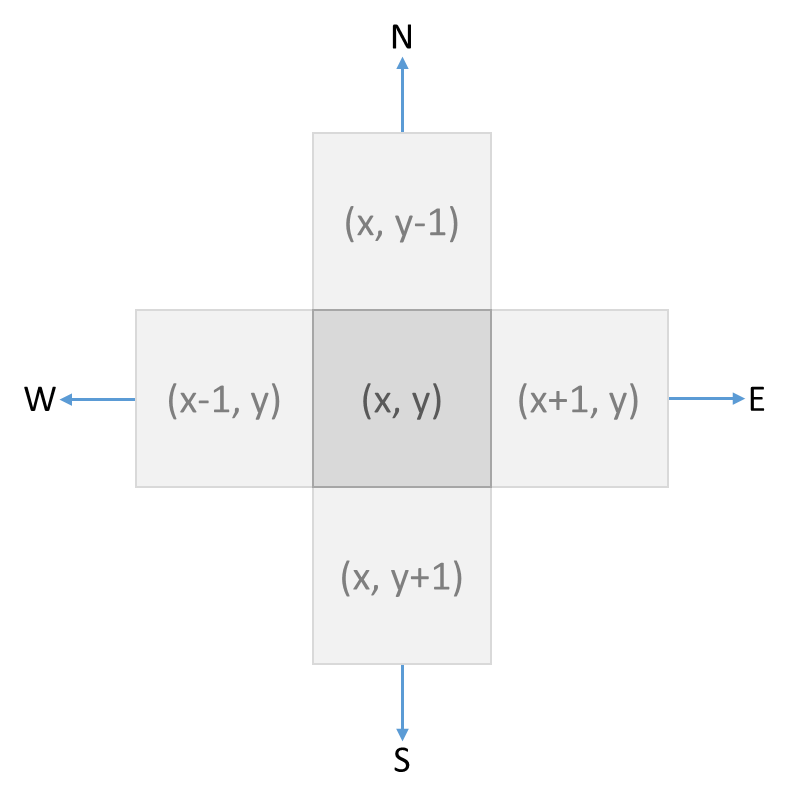
We denote the position of each cell in a grid with a pair of coordinates $$(x, y)$$ (tuple), where $$x \in \mathbb{N}$$ (int) is the column index and $$y$$ (int) is the row index. Each cell has four neighbors that are to the north (N), east (E), south (S) and west (W) of the cell. The directions in which these four neighbors are located relative to the cell are denoted with an uppercase letter (str), as indicated in the previous listing. This is the relationship between the coordinates of a cell and those of its neighbors:

Now, we can represent a possible fold of a protein as a sequence (str) of directions of neighboring cells where each next amino acid of the protein is found. As a convention, the first amino acid is at position $$(0, 0)$$ in the grid. The possible fold that we showed above on the left is then represented as SSSENEENWWN and corresponds to the positions of the consecutive amino acids shown below on the left. The possible fold that we showed above on the right is represented as SSENENENWWS and corresponds to the positions of the consecutive amino acids shown below on the right.

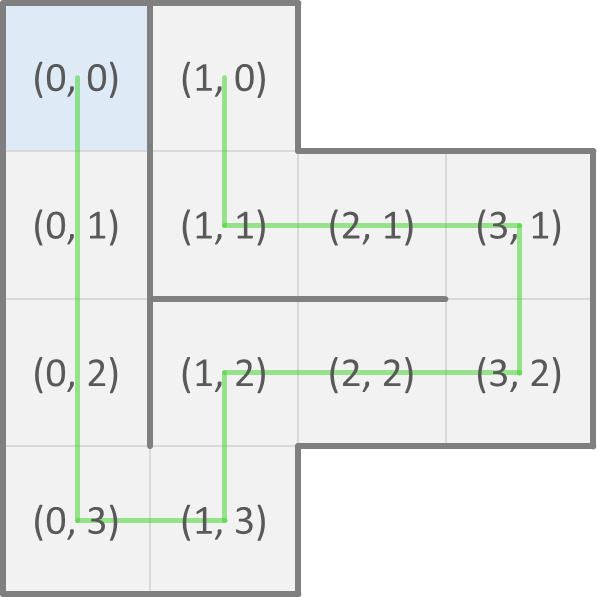
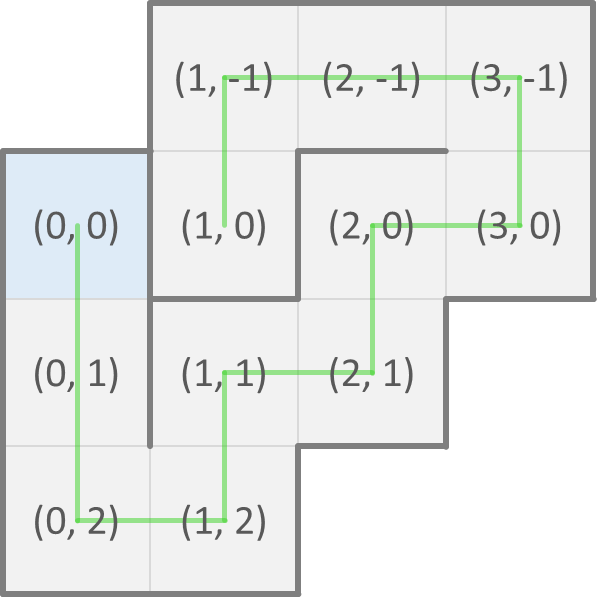
A fold that crosses itself (i.e. that visits the same cell of the grid twice) is invalid. Your task:

• Write a function positions that takes a possible fold (str) of a protein. The function must return a list with the positions of the consecutive amino acids in the given fold.

• Write a function fold that takes two arguments: i) a possible fold (str) of a protein and ii) the primary structure (str) of the protein. The function must return a dictionary (dict) that maps the position of each cell occupied in the given fold onto the classification of the amino acid in that cell.

• Write a function isneighbor that takes the positions of two cells in a grid. The function must return a Boolean value (bool) that indicates if the two cells are neighbors.

• Write a function contact_points that takes two arguments: i) a possible fold (str) of a protein and ii) the primary structure (str) of the protein. The function also has a third optional parameter model that may take a string (str) with two uppercase letters, that indicate if two neighboring cells must contain hydrophobic (H) or polar (P) amino acids (default value: 'HH'). The function must return the number (int) of neighboring cells in the given fold that have one cell belonging to one class of the model and the other cell belonging to the other class of the model. The order of the classes does not matter: in model='HH' both neighboring cells must contain hydrophobic amino acids, in model='PP' they must contain polar amino acids and in model='HP' and model='PH' (both models are equivalent) one cell must contain a hydrophobic amino acid and the other cell must contain a polar amino acid.

If the functions positions, fold and contact_points take a possible fold that is invalid, they must raise an AssertionError with the message invalid fold.

Example

>>> positions('SSSENEENWWN')
[(0, 0), (0, 1), (0, 2), (0, 3), (1, 3), (1, 2), (2, 2), (3, 2), (3, 1), (2, 1), (1, 1), (1, 0)]
>>> positions('SSENENENWWS')
[(0, 0), (0, 1), (0, 2), (1, 2), (1, 1), (2, 1), (2, 0), (3, 0), (3, -1), (2, -1), (1, -1), (1, 0)]
>>> positions('SSEENNWWWNW')
Traceback (most recent call last):
AssertionError: invalid fold

>>> fold('SSSENEENWWN', 'HHPPHHHPHHPH')
{(0, 0): 'H', (0, 1): 'H', (0, 2): 'P', (0, 3): 'P', (1, 3): 'H', (1, 2): 'H', (2, 2): 'H', (3, 2): 'P', (3, 1): 'H', (2, 1): 'H', (1, 1): 'P', (1, 0): 'H'}
>>> fold('SSENENENWWS', 'HHPPHHHPHHPH')
{(0, 0): 'H', (0, 1): 'H', (0, 2): 'P', (1, 2): 'P', (1, 1): 'H', (2, 1): 'H', (2, 0): 'H', (3, 0): 'P', (3, -1): 'H', (2, -1): 'H', (1, -1): 'P', (1, 0): 'H'}
>>> fold('SSEENNWWWNW', 'HHPPHHHPHHPH')
Traceback (most recent call last):
AssertionError: invalid fold

>>> isneighbor((3, 4), (4, 3))
False
>>> isneighbor((3, 4), (4, 4))
True

>>> contact_points('SSSENEENWWN', 'HHPPHHHPHHPH')
6
>>> contact_points('SSENENENWWS', 'HHPPHHHPHHPH')
9
>>> contact_points('SSSENEENWWN', 'HHPPHHHPHHPH', 'PP')
1
>>> contact_points('SSENENENWWS', 'HHPPHHHPHHPH', model='HP')
6
>>> contact_points('SSEENNWWWNW', 'HHPPHHHPHHPH')
Traceback (most recent call last):
AssertionError: invalid fold