Een Sudoku is een puzzel, typisch bestaande uit 81 vakjes, georganiseerd in 9 rijen en 9 kolommen. Bovendien is het 9x9 Sudoku-vierkant verder opgedeeld in 9 subblokken, van elk 3 rijen en 3 kolommen. In elk vakje moet een cijfer (1 t.e.m. 9) ingevuld worden, en hierbij gelden volgende beperkingen:
- in elke rij moet elk cijfer precies 1 keer voorkomen
- in elke kolom moet elk cijfer precies 1 keer voorkomen
- in elk subblok moet elk cijfer precies 1 keer voorkomen
Een Sudoku-puzzel bestaat uit een gedeeltelijk ingevuld 9x9 rooster, waarbij het de bedoeling is door verstandig tewerk te gaan, deze puzzel aan te vullen tot alle vakjes ingevuld zijn (met inachtname van de bovenstaande regels).

In deze oefening bouwen we een aantal klassen met het oog op het oplossen van Sudoku's.
Klasse Sudoku
Om de klasse Sudoku te programmeren, doe je best beroep op 2 lijsten, hierna de lijsten $$l$$ en $$o$$ genoemd. De lijst $$l$$ is een lijst van 9 lijsten, waarbij elke lijst een rij in de Sudoku voorstelt. Een 0 stelt hierbij een leeg vakje voor (m.a.w. een vakje waarvan de inhoud op dit moment nog niet ondubbelzinnig vastligt), en een cijfer 1 t.e.m. 9 stelt een vakje voor waarvan de inhoud met zekerheid gekend is (namelijk dit cijfer).Op die manier stemt de opgave uit onderstaande figuur overeen met de lijst
l = [[0, 0, 0, 2, 6, 0, 7, 0, 1],[6, 8, 0, 0, 7, 0, 0, 9, 0],[1, 9, 0, 0, 0, 4, 5, 0, 0],
[8, 2, 0, 1, 0, 0, 0, 4, 0], [0, 0, 4, 6, 0, 2, 9, 0, 0], [0, 5, 0, 0, 0, 3, 0, 2, 8],
[0, 0, 9, 3, 0, 0, 0, 7, 4], [0, 4, 0, 0, 5, 0, 0, 3, 6], [7, 0, 3, 0, 1, 8, 0, 0, 0]]
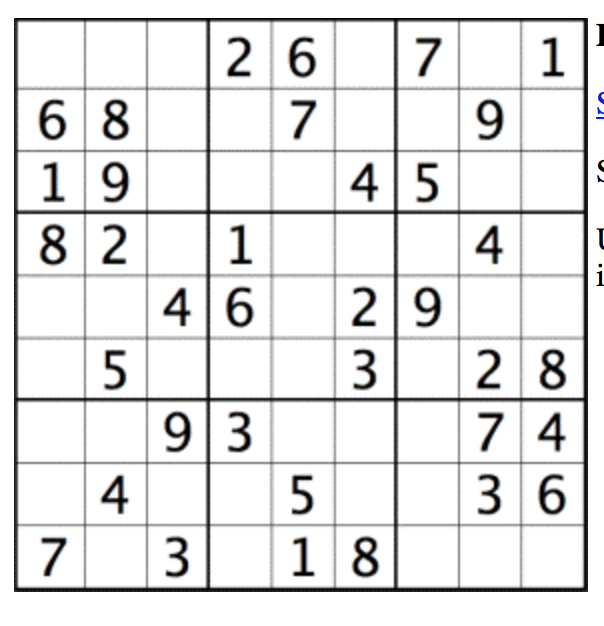
De lijst $$o$$ is opnieuw een lijst van 9 lijsten, en opnieuw stemt elke lijst overeen met een rij van de Sudoku-puzzel. Elk van de lijsten, bevat echter opnieuw een lijst. Deze lijst geeft aan welke mogelijkheden nog openstaan voor dit bepaald vakje. Zo geeft de lijst
o = [[[1], [2], [3, 4], [5, 4, 7], [8], [1, 2, 3, 5], [3, 6], [9], [7]], [...], ....]aan dat het eerste element van de eerste rij met zekerheid een 1 is, het tweede element met zekerheid een 2, en voor het derde element staan nog 2 opties open, namelijk de cijfers 3 en 4. Programmeer in deze klassen het volgende :
- een constructor met als enig argument de opgave van de Sudoku-puzzel. Deze opgave is een lijst van 9 lijsten. Elk van die lijsten bevat 9 getallen, en elk getal ligt tussen 0 en 9 (grenzen inbegrepen). Hierbij stelt een 0 een leeg vakje voor, terwijl een van nul verschillend getal een ingevuld vakje voorstelt (met dit cijfer).
- een methode `__str__()` die een stringgedaante van de puzzel genereert. Hierin worden regels onder elkaar afgebeeld, waarbij de vakjes door een spatie van elkaar gescheiden worden, en de regels door een `\n`-karakter. (De laatste regel eindigt dus NIET met een `\n`-karakter). Voor de puzzel die hierboven opgegeven werd, wordt dit dus:
0 0 0 2 6 0 7 0 1 6 8 0 0 7 0 0 9 0 1 9 0 0 0 4 5 0 0 8 2 0 1 0 0 0 4 0 0 0 4 6 0 2 9 0 0 0 5 0 0 0 3 0 2 8 0 0 9 3 0 0 0 7 4 0 4 0 0 5 0 0 3 6 7 0 3 0 1 8 0 0 0
- de methode
aantal_lege_vakjes()levert het totaal aantal lege vakjes in de puzzel (dus een geheel getal) - de methode
alle_opties()(zonder argumenten) levert een lijst in 3 dimensies. Dit is de lijst $$o$$ waarvan hoger sprake. Initieel komt die dus tot stand voor elk cijfer 0 in $$l$$ te vervangen door de lijst $$[1, 2, 3, 4, 5, 6, 7, 8, 9]$$ en elk ander cijfer door een lijst met als enig element dit cijfer. Naargelang de puzzel verder opgelost raakt, is het de bedoeling om tot steeds kortere lijsten voor elk vakje te komen. - de methode
aantal_opties()geeft het totaal aantal na te kijken mogelijkheden aan, gegeven de huidige lijst $$o$$. Dit is het product van de lengte van alle lijsten die in $$o$$ voorkomen. - de methode
is_mogelijk()heeft 1 argument, namelijk een lijst van 9 lijsten. Deze elementlijsten bevatten elk 9 getallen (en elk getal ligt tussen 1 en 9, grenzen inbegrepen). Het resultaat van de methode isTrueofFalsenaargelang het om een mogelijke oplossing gaat van de Sudoku, gegeven de huidige lijst $$o$$ van de puzzel. Je moet dus NIET nagaan of de gesuggereerde oplossing mogelijk is gegeven de Sudoku-regels maar WEL of het om een mogelijkheid gaat die nog te bekijken valt, gegeven de huidige inhoud van $$o$$.
Voorbeeld
puzzel = Sudoku([[0, 3, 5, 2, 6, 9, 7, 8, 1], [6, 8, 2, 5, 7, 1, 4, 9, 3], [0, 9, 7, 0, 3, 4, 5, 6, 2], [8, 2, 6, 1, 9, 5, 3, 4, 7], [3, 7, 4, 6, 8, 2, 9, 1, 5], [9, 5, 1, 7, 4, 3, 6, 2, 8], [5, 1, 9, 0, 2, 6, 8, 7, 4], [2, 4, 8, 9, 5, 7, 1, 3, 6], [0, 6, 3, 4, 1, 8, 2, 5, 9]])# doctest: +NEWCONTEXT print(puzzel) #0 3 5 2 6 9 7 8 1 #6 8 2 5 7 1 4 9 3 #0 9 7 0 3 4 5 6 2 #8 2 6 1 9 5 3 4 7 #3 7 4 6 8 2 9 1 5 #9 5 1 7 4 3 6 2 8 #5 1 9 0 2 6 8 7 4 #2 4 8 9 5 7 1 3 6 #0 6 3 4 1 8 2 5 9 puzzel.aantal_lege_vakjes() #5 puzzel.aantal_opties() #59049 puzzel.alle_opties() #[[[1, 2, 3, 4, 5, 6, 7, 8, 9], [3], [5], [2], [6], [9], [7], [8], [1]], [[6], [8], [2], [5], [7], [1], [4], [9], [3]], [[1, 2, 3, 4, 5, 6, 7, 8, 9], [9], [7], [1, 2, 3, 4, 5, 6, 7, 8, 9], [3], [4], [5], [6], [2]], [[8], [2], [6], [1], [9], [5], [3], [4], [7]], [[3], [7], [4], [6], [8], [2], [9], [1], [5]], [[9], [5], [1], [7], [4], [3], [6], [2], [8]], [[5], [1], [9], [1, 2, 3, 4, 5, 6, 7, 8, 9], [2], [6], [8], [7], [4]], [[2], [4], [8], [9], [5], [7], [1], [3], [6]], [[1, 2, 3, 4, 5, 6, 7, 8, 9], [6], [3], [4], [1], [8], [2], [5], [9]]] puzzel.is_mogelijk([[4, 3, 5, 2, 6, 9, 7, 8, 1], [6, 8, 2, 5, 7, 1, 4, 9, 3], [1, 9, 7, 8, 3, 4, 5, 6, 2], [8, 2, 6, 1, 9, 5, 3, 4, 7], [3, 7, 4, 6, 8, 2, 9, 1, 5], [9, 5, 1, 7, 4, 3, 6, 2, 8], [5, 1, 9, 3, 2, 6, 8, 7, 4], [2, 4, 8, 9, 5, 7, 1, 3, 6], [7, 6, 3, 4, 1, 8, 2, 5, 9]]) #True puzzel.is_mogelijk([[4, 3, 5, 2, 6, 9, 7, 8, 1], [6, 8, 2, 5, 7, 1, 4, 9, 3], [1, 9, 7, 8, 3, 4, 5, 6, 2], [8, 2, 6, 1, 9, 5, 3, 4, 7], [3, 7, 4, 6, 8, 2, 9, 1, 5], [9, 5, 1, 7, 4, 3, 6, 2, 8], [5, 1, 9, 3, 2, 6, 8, 7, 4], [2, 4, 8, 9, 7, 7, 1, 3, 6], [7, 5, 3, 4, 1, 8, 2, 5, 9]]) #False
Klasse Snoeier
Dit is een basisklasse, bedoeld om het aantal mogelijke oplossingen van een Sudoku-puzzel te beperken (dus te snoeien in alle kandidaat-oplossingen). Programmeer in deze basisklasse het onderstaande:- een constructor met 1 argument, een natuurlijk getal (de betekenis van dit getal wordt verder verduidelijkt in de beschrijving van klassen die overerven van
de klasse
Snoeier) - een methode
snoei_1D()met als argument een lijst van 9 lijsten. Elk van deze lijsten heeft minstens de lengte 1, en bevat enkel getallen 1 t.e.m. 9 en bevat geen dubbels en is van klein naar groot gesorteerd. De methode levert geen onmiddellijk resultaat (dus typeNone) maar past de argumentlijst aan, zoals hieronder weergegeven:- overloop elk element $$e$$ van de originele argumentlijst in de gegeven volgorde
- indien $$e$$ uit 1 element bestaat, schrap je de waarde $$e[0]$$ uit alle andere elementen van de argumentlijst
Klasse RijSnoeier
Deze klasse snoeit in een lijst $$o$$ kandidaatoplossingen door enkel de rij $$n$$ van de puzzel te bekijken, en hierin te snoeien. Programmeer in deze klasse, die overerft van de klasseSnoeier:
- een constructor met 1 argument, een natuurlijk getal $$n$$
- de methode `__str__()` levert de string
Rn(dus de letter R gevolgd door het natuurlijk getal $$n$$, bv.R5 - een methode
snoei()met als argument een lijst $$o$$ (dus een lijst die alle te beschouwen oplossingen van een Sudoku-puzzel voorstelt). Deze methode levert geen returnwaarde (dus typeNone) maar past de lijst $$o$$ aan, door te snoeien in de rij $$n$$ van de puzzel. Hiertoe haal je deze rij uit de argumentlijst, en gebruik je de methodesnoei_1D()uit de klasseSnoeierom het aantal oplossingen te reduceren.
Klasse KolomSnoeier
Deze klasse heeft dezelfde methoden als de klasseRijSnoeier met onderstaande aanpassingen:
- de methode `__str__()` levert nu de string
Kn - de methode
snoei()bekijkt nu de $$n$$-de kolom van de puzzel om te snoeien in het aantal kandidaatoplossingen
Klasse BlokSnoeier
Deze klasse heeft dezelfde methoden als de klasseRijSnoeier met onderstaande aanpassingen:
- de methode `__str__()` levert nu de string
Bn - de methode
snoei()bekijkt nu de $$n$$-de blok van de puzzel om te snoeien in het aantal kandidaatoplossingen
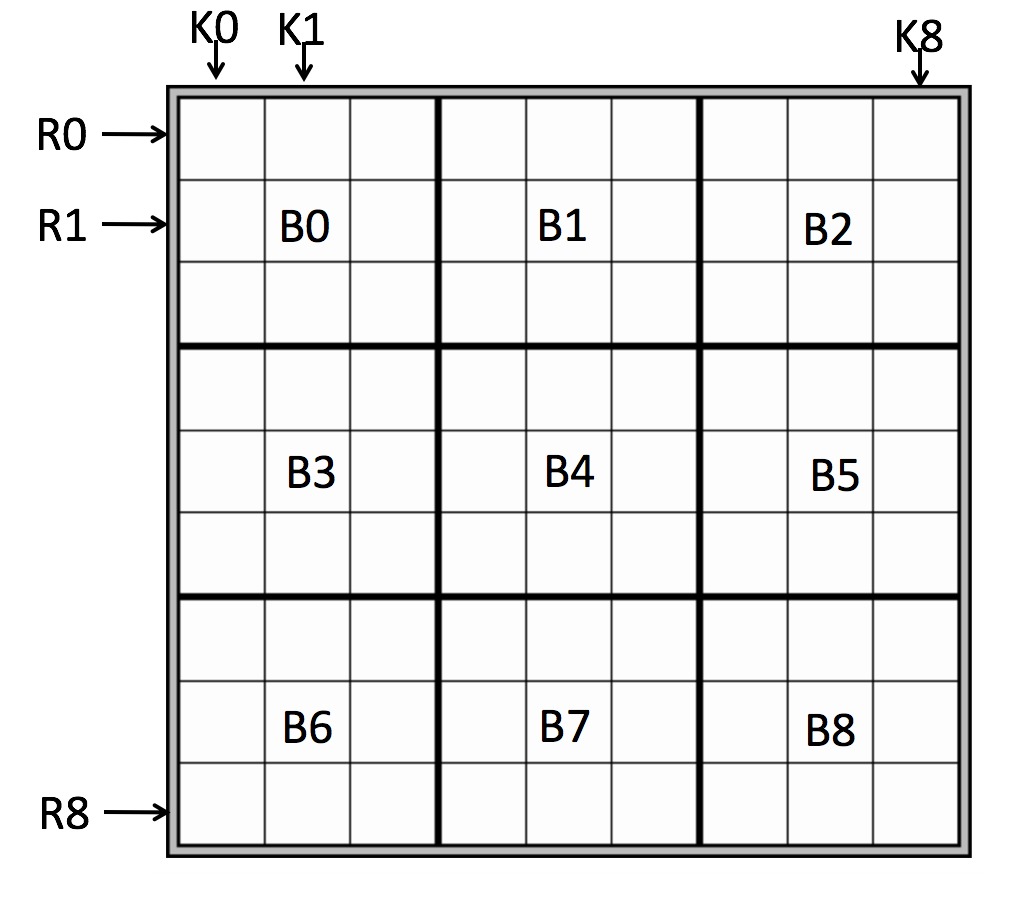
Voorbeeld
basis = Snoeier(0)# doctest: +NEWCONTEXT l = [[4], [3], [5], [2], [6], [9], [3, 5, 7, 8, 9], [8], [1]] basis.snoei_1D(l) print(l) #[[4], [3], [5], [2], [6], [9], [7], [8], [1]] rij_snoeier = RijSnoeier(8) print(rij_snoeier) #R8 r = [[[4], [3], [5], [2], [6], [9], [7], [8], [1]], [[6], [8], [2], [5], [7], [1], [4], [9], [3]], [[1], [9], [7], [8], [3], [4], [5], [6], [2]], [[8], [2], [6], [1], [9], [5], [3], [4], [7]], [[3], [7], [4], [6], [8], [2], [9], [1], [5]], [[9], [5], [1], [7], [4], [3], [6], [2], [8]], [[5], [1], [9], [3], [2], [6], [8], [7], [4]], [[2], [4], [8], [9], [5], [7], [1], [3], [6]], [[7], [2, 4, 5, 7, 8], [1, 3, 5, 8, 9], [4], [1], [8], [2], [5], [9]]] rij_snoeier.snoei(r) print(r) #[[[4], [3], [5], [2], [6], [9], [7], [8], [1]], [[6], [8], [2], [5], [7], [1], [4], [9], [3]], [[1], [9], [7], [8], [3], [4], [5], [6], [2]], [[8], [2], [6], [1], [9], [5], [3], [4], [7]], [[3], [7], [4], [6], [8], [2], [9], [1], [5]], [[9], [5], [1], [7], [4], [3], [6], [2], [8]], [[5], [1], [9], [3], [2], [6], [8], [7], [4]], [[2], [4], [8], [9], [5], [7], [1], [3], [6]], [[7], [], [3], [4], [1], [8], [2], [5], [9]]] kolom_snoeier = KolomSnoeier(2) print(kolom_snoeier) #K2 k = [[[4], [3], [2, 4, 5, 8, 9], [2], [6], [9], [7], [8], [1]], [[6], [8], [2], [5], [7], [1], [4], [9], [3]], [[1], [2, 3, 9], [7], [8], [3], [4], [5], [1, 2, 4, 5, 6, 7, 9], [2]], [[8], [2], [1, 4, 7, 8, 9], [1], [9], [5], [3], [4], [2, 3, 5, 7, 8]], [[3], [7], [4], [6], [8], [2], [9], [1], [5]], [[9], [5], [1, 2, 5, 6, 7, 9], [7], [4], [3], [6], [2], [2, 3, 4, 5, 6, 7, 8, 9]], [[5], [1], [1, 2, 3, 4, 5, 8, 9], [3], [2], [6], [8], [7], [4]], [[2], [4], [8], [9], [5], [7], [1], [3], [6]], [[7], [6], [4, 5, 7, 9], [4], [1], [1, 2, 5, 9], [2], [5], [9]]] kolom_snoeier.snoei(k) print(k) #[[[4], [3], [5, 9], [2], [6], [9], [7], [8], [1]], [[6], [8], [2], [5], [7], [1], [4], [9], [3]], [[1], [2, 3, 9], [7], [8], [3], [4], [5], [1, 2, 4, 5, 6, 7, 9], [2]], [[8], [2], [1, 9], [1], [9], [5], [3], [4], [2, 3, 5, 7, 8]], [[3], [7], [4], [6], [8], [2], [9], [1], [5]], [[9], [5], [1, 5, 6, 9], [7], [4], [3], [6], [2], [2, 3, 4, 5, 6, 7, 8, 9]], [[5], [1], [1, 3, 5, 9], [3], [2], [6], [8], [7], [4]], [[2], [4], [8], [9], [5], [7], [1], [3], [6]], [[7], [6], [5, 9], [4], [1], [1, 2, 5, 9], [2], [5], [9]]] blok_snoeier = BlokSnoeier(3) print(blok_snoeier) #B3 b = [[[4], [3], [5], [2], [6], [9], [7], [8], [1]], [[6], [8], [2], [5], [7], [1], [4], [9], [3]], [[1], [9], [7], [8], [3], [4], [5], [6], [2]], [[8], [2, 3, 4, 5, 6, 7, 8, 9], [2, 3, 4, 5, 7, 8, 9], [1], [9], [5], [3], [4], [7]], [[3], [7], [4], [6], [8], [2], [9], [1], [5]], [[9], [2, 3, 6, 8, 9], [1], [7], [4], [3], [6], [2], [8]], [[5], [1], [9], [3], [2], [6], [8], [7], [4]], [[2], [4], [8], [9], [5], [7], [1], [3], [6]], [[7], [6], [3], [4], [1], [8], [2], [5], [9]]] blok_snoeier.snoei(b) print(b) #[[[4], [3], [5], [2], [6], [9], [7], [8], [1]], [[6], [8], [2], [5], [7], [1], [4], [9], [3]], [[1], [9], [7], [8], [3], [4], [5], [6], [2]], [[8], [2, 5, 6], [2, 5], [1], [9], [5], [3], [4], [7]], [[3], [7], [4], [6], [8], [2], [9], [1], [5]], [[9], [2, 6], [1], [7], [4], [3], [6], [2], [8]], [[5], [1], [9], [3], [2], [6], [8], [7], [4]], [[2], [4], [8], [9], [5], [7], [1], [3], [6]], [[7], [6], [3], [4], [1], [8], [2], [5], [9]]]
Klasse Sudoku : oplossen van de puzzel
We voegen nu drie methoden toe aan de klasse Sudoku die je hierboven geprogrammeerd hebt.- de methode
snoei()met 1 argument, een object van een klasse die overerft van de klasseSnoeier(je mag ervan uitgaan dat dit object dus over een methodesnoei()beschikt, zoals hierboven aangegeven in de klassenRijSnoeier,KolomSnoeierenBlokSnoeier. Na oproep is de lijst $$o$$ gesnoeid, gebruik makend van desnoei()-methode van het argumentobject. Daarnaast is ook de $$l$$-lijst aangepast, is zijn de vakjes waarvoor niet langer twijfel bestaat, ingevuld met een cijfer verschillend van 0. - de methode
snoei_lijst()heeft als enig argument een lijst van snoei-objecten. Het resultaat van deze methode is dat alle snoei-objecten in de argumentlijst opgeroepen worden, en dat de lijst $$l$$ aangepast wordt zodat vakjes waarvoor geen twijfel meer bestaat, ingevuld worden met een cijfer verschillend van 0. De snoei-objecten worden 1 maal opgeroepen, in de volgorder waarin ze in de lijst voorkomen. - de methode
los_op()heeft ook als enig argument een lijst van snoei-objecten $$s$$. Deze methode roept de hierboven beschreven methodesnoei_lijst()op, met als argument de lijst $$s$$. Dit wordt herhaald tot het totaal aantal te beschouwen kandidaatoplossingen niet meer zakt.
Voorbeeld
puzzel = Sudoku([[4, 3, 5, 2, 6, 9, 7, 8, 1], [6, 8, 2, 5, 7, 1, 4, 9, 3], [1, 9, 7, 8, 3, 4, 5, 6, 2], [8, 0, 6, 0, 9, 5, 3, 4, 0], [3, 7, 4, 6, 8, 2, 9, 1, 5], [9, 5, 1, 7, 4, 3, 6, 2, 8], [5, 0, 0, 0, 2, 0, 8, 7, 4], [2, 4, 8, 9, 5, 7, 1, 3, 6], [7, 6, 3, 4, 1, 8, 2, 5, 9]]) rij_snoeiers = [RijSnoeier(i) for i in [6, 3]] kolom_snoeiers = [KolomSnoeier(i) for i in []] blok_snoeiers = [BlokSnoeier(i) for i in []] print(puzzel.alle_opties()) #[[[4], [3], [5], [2], [6], [9], [7], [8], [1]], [[6], [8], [2], [5], [7], [1], [4], [9], [3]], [[1], [9], [7], [8], [3], [4], [5], [6], [2]], [[8], [1, 2, 3, 4, 5, 6, 7, 8, 9], [6], [1, 2, 3, 4, 5, 6, 7, 8, 9], [9], [5], [3], [4], [1, 2, 3, 4, 5, 6, 7, 8, 9]], [[3], [7], [4], [6], [8], [2], [9], [1], [5]], [[9], [5], [1], [7], [4], [3], [6], [2], [8]], [[5], [1, 2, 3, 4, 5, 6, 7, 8, 9], [1, 2, 3, 4, 5, 6, 7, 8, 9], [1, 2, 3, 4, 5, 6, 7, 8, 9], [2], [1, 2, 3, 4, 5, 6, 7, 8, 9], [8], [7], [4]], [[2], [4], [8], [9], [5], [7], [1], [3], [6]], [[7], [6], [3], [4], [1], [8], [2], [5], [9]]] print(puzzel.aantal_opties()) #4782969 puzzel.snoei(rij_snoeiers[0]) print(puzzel.aantal_opties()) #186624 puzzel.snoei_lijst(rij_snoeiers) print(puzzel.aantal_opties()) #6912 print(puzzel) 4 3 5 2 6 9 7 8 1 6 8 2 5 7 1 4 9 3 1 9 7 8 3 4 5 6 2 8 0 6 0 9 5 3 4 0 3 7 4 6 8 2 9 1 5 9 5 1 7 4 3 6 2 8 5 0 0 0 2 0 8 7 4 2 4 8 9 5 7 1 3 6 7 6 3 4 1 8 2 5 9 puzzel.snoei_lijst(kolom_snoeiers) print(puzzel.aantal_opties()) #6912