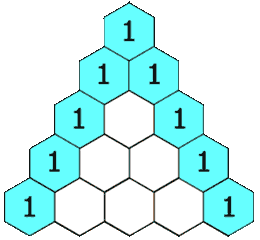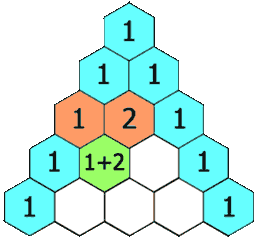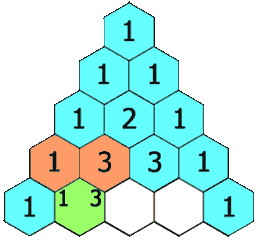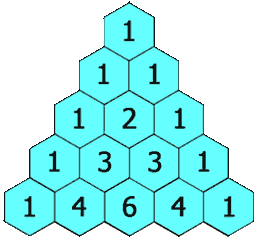
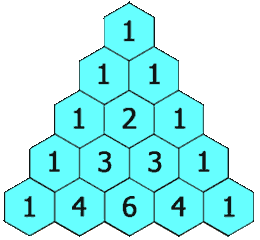
You may have heard of Pascal's triangle before. A triangular array that is constructed in the following way. At the top of the triangle you write the number 1. Each next row of the triangle is constructed by adding the number above and to the left with the number above and to the right of each cell in the row to find the new value in that cell. If either the number to the right or left is not present, substitute a zero in its place. Below we demonstrate how the first five rows of the triangle are constructed.

However, few people know that it would historically be more correct to talk about Pascal's square. Blaise Pascal (1623-1662) — the French mathematician after which the triangle was named — arranged the numbers himself in the form of a square. The construction of the square is analogous to that of the triangle. Pick a number $$n \in \mathbb{N}_0$$. Fill all positions on the top row and the left column with that number $$n$$. Traverse all other cells of the square from left to right and from top to bottom, and fill each cell with the sum of the numbers in the two neighboring cells to the left and on top. Below we show Pascal's square with four rows and four columns, with $$n = 1$$.

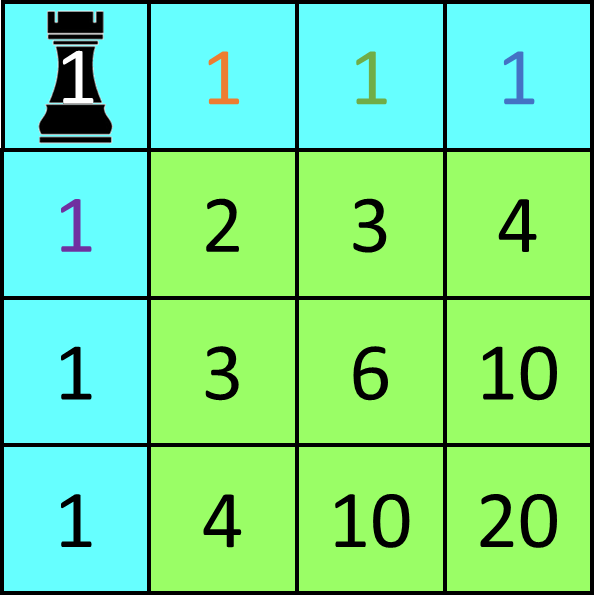
A property of Pascal's square (resp. triangle) is that each cell displays the number of distinct paths that lead to that cell from the upper left cell of the square (resp. top cell of the triangle), assuming only rightward and downward (resp. left down and right down) movements are allowed. So, in the square given above, the cell marked 4 in the second row, fourth column, can be reached in four ways: 1–1–1–4, 1–1–3–4, 1–2–3–4 and 1–2–3–4.

Assignment

• Write a function square that takes an integer $$m \in \mathbb{N}_0$$ as its argument. The function also has a second optional parameter that takes an integer $$n \in \mathbb{N}_0$$ (default value: $$n=1$$). The function must return a list of lists that represents Pascal's square with $$m$$ rows and $$m$$ columns, whose top row and left column are filled with the number $$n$$.

• Write a function routes that takes an integer $$m \in \mathbb{N}_0$$ as its argument. The function also has a second optional parameter that takes an integer $$n \in \mathbb{N}_0$$ (default value: $$n=1$$). The function must return a string representation of Pascal's square with $$m$$ rows and $$m$$ columns, whose top row and left column are filled with the number $$n$$. In this string representation, each number must be right justified over $$p + 1$$ positions, with $$p$$ being the number of digits in the value at the bottom right of the square.

Example

>>> square(3)
[[1, 1, 1], [1, 2, 3], [1, 3, 6]]
>>> square(3, 100)
[[100, 100, 100], [100, 200, 300], [100, 300, 600]]
>>> square(4)
[[1, 1, 1, 1], [1, 2, 3, 4], [1, 3, 6, 10], [1, 4, 10, 20]]

>>> print(routes(3))
 1 1 1
 1 2 3
 1 3 6
>>> print(routes(3, 100))
 100 100 100
 100 200 300
 100 300 600
>>> print(routes(4))
  1  1  1  1
  1  2  3  4
  1  3  6 10
  1  4 10 20
>>> print(routes(6))
   1   1   1   1   1   1
   1   2   3   4   5   6
   1   3   6  10  15  21
   1   4  10  20  35  56
   1   5  15  35  70 126
   1   6  21  56 126 252
>>> print(routes(8))
	1    1    1    1    1    1    1    1
	1    2    3    4    5    6    7    8
	1    3    6   10   15   21   28   36
	1    4   10   20   35   56   84  120
	1    5   15   35   70  126  210  330
	1    6   21   56  126  252  462  792
	1    7   28   84  210  462  924 1716
	1    8   36  120  330  792 1716 3432
>>> print(routes(10))
	 1     1     1     1     1     1     1     1     1     1
	 1     2     3     4     5     6     7     8     9    10
	 1     3     6    10    15    21    28    36    45    55
	 1     4    10    20    35    56    84   120   165   220
	 1     5    15    35    70   126   210   330   495   715
	 1     6    21    56   126   252   462   792  1287  2002
	 1     7    28    84   210   462   924  1716  3003  5005
	 1     8    36   120   330   792  1716  3432  6435 11440
	 1     9    45   165   495  1287  3003  6435 12870 24310
	 1    10    55   220   715  2002  5005 11440 24310 48620