Imprecisie/standard error

Het feit dat het steekproefgemiddelde (over een groot aantal vergelijkbare studies) gemiddeld gezien niet afwijkt van de gezochte waarde \(\mu\), impliceert niet dat ze niet rond die waarde varieert. Om inzicht te krijgen hoe dicht we het steekproefgemiddelde bij \(\mu\) mogen verwachten, wensen we bijgevolg ook haar variabiliteit te kennen.

We illustreren dit met de NHANES studie

We zullen 15 vrouwen willekeurig selecteren uit de NHANES studie en zullen hun lengte registreren.
We herhalen dit 50 keer om de variatie van steekproef tot steekproef te beoordelen
We plotten de boxplot voor iedere steekproef en duiden het gemiddelde aan.

set.seed(2105)
library(NHANES)

fem <- NHANES %>%
  filter(Gender=="female" & !is.na(DirectChol)) %>%
  select("DirectChol")

n <- 15 # number of subjects per sample
nSim <- 50 # number of simulations

femSamp <- matrix(nrow=n,ncol=nSim)
for (j in 1:nSim)
{
  femSamp[,j] <- sample(fem$DirectChol,15)
  if (j<4) {
    p <- femSamp %>%
      log2 %>%
      data.frame %>%
      gather("sample","log2cholesterol") %>%
      ggplot(aes(x=sample,y=log2cholesterol)) +
      geom_boxplot() +
      stat_summary(
        fun.y=mean,
        geom="point",
        shape=19,
        size=3,
        color="red",
        fill="red") +
      geom_hline(yintercept = mean(fem$DirectChol %>% log2)) +
      ylab("cholesterol (log2)")
    print(p)
  }
}

femSamp %>%
  log2 %>%
  data.frame %>%
  gather("sample","log2cholesterol") %>%
  ggplot(aes(x=sample,y=log2cholesterol)) +
  geom_boxplot() +
  stat_summary(fun.y=mean, geom="point", shape=19, size=3, color="red", fill="red") +
  geom_hline(yintercept = mean(fem$DirectChol %>% log2)) +
  ylab("cholesterol (log2)")

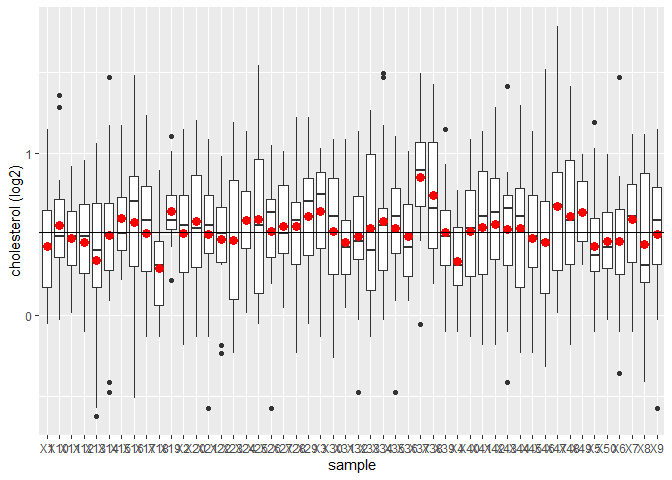
We observeren dat het steekproefgemiddelde fluctueert rond het gemiddelde van de populatie.

Hoe doen we dit op basis van een enkele steekproef?

Om inzicht te krijgen in de variabiliteit op \(\bar X\) op basis van een enkele steekproef zullen we assumpties moeten maken:

We zullen ervan uitgaan dat de metingen \(X_1, X_2, ..., X_n\) werden gemaakt bij \(n\) onafhankelijke observationele eenheden. In woorden betekent onafhankelijkheid dat elk subject een volledig nieuw stukje informatie bijdraagt tot het geheel. Een voorbeeld van afhankelijkheid tussen studie-objecten komt klassiek uit de studie van kankerverwekkende stoffen. Bij testen op zwangere ratten, worden metingen gedaan op hun levende foetussen of boorlingen. Foetussen van eenzelfde moeder delen dezelfde genetische achtergrond en zijn daarom waarschijnlijk meer aan elkaar gelijk dan foetussen van verschillende moeders. Zelfs al zijn de moeders die opgenomen worden in zo’n studie onafhankelijk van elkaar gekozen, de verschillende kleine ratjes leveren niet langer onafhankelijke stukjes informatie: via de gedeelde moeders is een afhankelijkheid ingebouwd.

Afhankelijke gegevens worden ondermeer ook verzameld in pre-test/post-test designs en cross-over studies.

Voor de Captopril studie bijvoorbeeld hebben we afhankelijke observaties

Bloeddrukmetingen voor (\(Y_{i,before}\)) en na (\(Y_{i,after}\)) toediening van captopril aan dezelfde patiënt \(i=1,\ldots,n\).
We hebben ze omgezet in n onafhankelijke metingen door het verschil \(Y_{i,na}-Y_{i,voor}\) te nemen.

De volgende eigenschap illustreert de noodzaak om over onafhankelijke gegevens te beschikken, wil men gemakkelijk de variabiliteit van het steekproefgemiddelde kunnen bepalen.

Eigenschap

Als \(X\) en \(Y\) onafhankelijke toevalsveranderlijken zijn, dan geldt:

\[\begin{equation*} \text{Var}(X+Y) = \text{Var}(X) + \text{Var}(Y) \end{equation*}\]

Algemeen (d.i. voor mogelijks afhankelijke toevalsveranderlijken \(X\) en \(Y\)) geldt voor constanten \(a\) en \(b\):

\[\begin{eqnarray*} \text{Var}(aX+bY) &=& a^2 \text{Var}(X) + b^2 \text{Var}(Y) + 2 ab {% \text{Cor}}(X,Y)\sqrt{\text{Var}(X)}\sqrt{\text{Var}(Y)} \end{eqnarray*}\]

Einde Eigenschap

Een veelgemaakte fout is dat men beweert dat \(\text{Var}(X-Y)=\text{Var}(X)-\text{Var}(Y)\). Niets is minder waar! Stel bijvoorbeeld dat de lengte \(X\) van moeders en de lengte \(Y\) van vaders evenveel variëren zodat \(\text{Var}(X)=\text{Var}(Y)\). Dan impliceert dat nog niet dat als je het verschil \(X-Y\) neemt tussen de lengte van een moeder en haar partner, dat dit verschil variantie nul heeft; d.w.z. dat het niet varieert en bijgevolg voor alle moeder-vader paren exact dezelfde waarde aanneemt! Bovenstaande formules geven inderdaad integendeel aan dat:

\[\begin{equation*} \text{Var}(X-Y) = \text{Var}(X) + \text{Var}(Y) -2{\text{Cor}}(X,Y)\sqrt{\text{Var}(X)}\sqrt{\text{Var}(Y)}. \end{equation*}\]

Variantie schatter voor \(\bar X\)

Gebruik makend van deze rekenregels en steunend op de onafhankelijkheid van de observaties (waarvan we gebruik maken in de derde overgang, *) kunnen we nu verder berekenen dat:

\[\begin{eqnarray*} \text{Var}(\bar X)&=&\text{Var} \left(\frac{X_1+ X_2+ ... + X_n}{n}\right) \\ &= & \frac{\text{Var} (X_1+ X_2+ ... + X_n)}{n^2} \\ &\overset{*}{=} & \frac{\text{Var}(X_1)+ \text{Var}(X_2)+ ... + \text{Var}(X_n)}{n^2} \\ &=& \frac{\sigma^2 + \sigma^2 + ... \sigma^2}{n^2} \\ &= & \frac{\sigma^2}{n}. \end{eqnarray*}\]

Het steekproefgemiddelde heeft dus een spreiding (standaarddeviatie) rond haar gemiddelde \(\mu\) die \(\sqrt{n}\) keer kleiner is dan de deviatie op de oorspronkelijke observaties. Vandaar dat we meer over \(\mu\) kunnen leren door het steekproefgemiddelde \(\bar X\) te observeren dan door een individuele waarde \(X\) te observeren.

Definitie 23: (Standaard error)

De standaarddeviatie van \(\bar{X}\) is \(\sigma/\sqrt{n}\) en krijgt in de literatuur de speciale naam {standard error} van het gemiddelde. Algemeen noemt men de standaarddeviatie van een schatter voor een bepaalde parameter \(\theta\), de standard error van die schatter. Men noteert dit als \(SE\).

Einde definitie

Voorbeeld 23: (Gemiddelde bloeddrukverandering)

Stel dat we \(n = 15\) systolische bloeddrukobservaties zullen meten en dat de standaarddeviatie van de bloeddrukverschillen in de populatie \(\sigma = 9.0\) mmHg bedraagt, dan is standard error (SE) van de systolische bloeddrukveranderingen \(\bar X\):

\[SE= \frac{9.0}{\sqrt{15}}=2.32\text{mmHg.}\]

Meestal is \(\sigma\), en bijgevolg de standard error van het steekproefgemiddelde, ongekend. Men moet dan de standard error schatten. Een voor de hand liggende schatter met goede eigenschappen is \(S/\sqrt{n},\) waarbij \(S^2\) de steekproefvariantie van de reeks observaties \(X_1,...,X_n\) is en \(S\) de steekproef standaarddeviatie wordt genoemd.

Voor het captopril voorbeeld kunnen we de standard error op het steekproefgemiddelde van de bloeddrukveranderingen schatten in R als

n <- length(delta)
se <- sd(delta)/sqrt(n)
se

## [1] 2.330883

Standaarddeviatie vs standard error

We illustreren dit opnieuw a.d.h.v. herhaalde steekproeven:

Verschillende steekproef groottes: 10, 50, 100
Neem 1000 steekproeven per steekproef grootte van de NHANES studie, voor iedere steekproef berekenen we:
- Het gemiddelde
- De steekproefstandaarddeviatie
- de standaard error
We maken een boxplot van de steekproefstandaardevaties en de standaard errors voor de verschillende steekproefgroottes
In plaats van een for loop te gebruiken zullen we de sapply functie gebruiken die efficiënter is. Het neemt een vector of lijst als invoer en past de functie toe op ieder element van de vector of lijst.

set.seed(24)
femSamp10 <- sapply(
  1:1000,
  function(j,x,size) sample(x,size),
  size=10,
  x=fem$DirectChol)

femSamp50 <- sapply(
  1:1000,
  function(j,x,size) sample(x,size),
  size=50,
  x=fem$DirectChol)

femSamp100 <- sapply(
  1:1000,
  function(j,x,size) sample(x,size),
  size=100,
  x=fem$DirectChol)

res<-rbind(
  femSamp10 %>%
    log2%>%
    as.data.frame %>%
    gather(sample,log2Chol) %>%
    group_by(sample)%>%
    summarize_at("log2Chol",
               list(median=~median(.,na.rm=TRUE),
                    mean=~mean(.,na.rm=TRUE),
                    sd=~sd(.,na.rm=TRUE),
                    n=function(x) x%>%is.na%>%`!`%>%sum)) %>%
    mutate(se=sd/sqrt(n)) ,

  femSamp50 %>%
    log2 %>%  
    as.data.frame %>%
    gather(sample,log2Chol) %>%
    group_by(sample)%>%
    summarize_at("log2Chol",
               list(median=~median(.,na.rm=TRUE),
                    mean=~mean(.,na.rm=TRUE),
                    sd=~sd(.,na.rm=TRUE),
                    n=function(x) x%>%is.na%>%`!`%>%sum)) %>%
    mutate(se=sd/sqrt(n)),

  femSamp100 %>%
    log2 %>%
    as.data.frame %>%
    gather(sample,log2Chol) %>%
    group_by(sample)%>%
    summarize_at("log2Chol",
               list(median=~median(.,na.rm=TRUE),
                    mean=~mean(.,na.rm=TRUE),
                    sd=~sd(.,na.rm=TRUE),
                    n=function(x) x%>%is.na%>%`!`%>%sum)) %>%
    mutate(se=sd/sqrt(n))
  )

Gemiddelden

We illustreren de impact van steekproefgrootte op de distributie van de gemiddeldes van verschillende steekproeven

res %>%
  ggplot(aes(x= n %>% as.factor,y = mean)) +
  geom_boxplot() +
  ylab("Direct cholesterol (log2)") +
  xlab("sample size")

Merk op dat de variatie van de steekproefgemiddelden inderdaad afneemt naarmate de steekproefgrootte toeneemt. De schatting wordt dus nauwkeuriger naarmate de steekproefgrootte toeneemt.

Standard deviatie

We illustreren nu de impact van de steekproefgrootte op de verdeling van de standaarddeviatie van de verschillende steekproeven

res %>%
  ggplot(aes(x=n%>%as.factor,y=sd)) +
  geom_boxplot() +
  ylab("standard deviation") +
  xlab("sample size")

De standaarddeviatie blijft vergelijkbaar voor de steekproefgroottes. Het is gecentreerd rond dezelfde waarde: de standaarddeviatie in de populatie. Het vergroten van de steekproefgrootte heeft inderdaad geen invloed op de variabiliteit in de populatie!
Opnieuw zien we dat de variabiliteit van de standaarddeviatie afneemt naarmate de steekproefgrootte toeneemt. De standaarddeviatie kan dus ook nauwkeuriger worden geschat naarmate de steekproefgrootte toeneemt.

Standaard error van het gemiddelde

Ten slotte illustreren we de impact van de steekproefgrootte op de verdeling van de standaarddeviatie van het gemiddelde van de verschillende steekproeven, de standaard error.

res %>%
ggplot(aes(x=n%>%as.factor,y=se)) +
geom_boxplot() +
ylab("standard error") +
xlab("sample size")

De standaard error (de schatter voor de nauwkeurigheid van het steekproefgemiddelde) vermindert aanzienlijk naarmate de steekproefgrootte toeneemt, wat opnieuw bevestigt dat de schatting van het steekproefgemiddelde nauwkeuriger wordt.

Normaal verdeelde gegevens

Als de gegevens Normaal verdeeld zijn, dan zijn er meerdere onvertekende schatters voor het populatiegemiddelde \(\mu\), bvb. het steekproefgemiddelde en de mediaan. Men kan echter aantonen dat in dat geval het steekproefgemiddelde \(\bar{X}\) de onvertekende schatter is voor \(\mu\) met de kleinste standard error. Dat betekent dat ze gemiddeld minder afwijkt van de echte parameterwaarde dan de mediaan, die veel meer varieert van steekproef tot steekproef. Het steekproefgemiddelde is bijgevolg een schatter die accuraat is (want onvertekend) en meest precies (kleinste standaarddeviatie).

We illustreren dit voor herhaalde steekproeven met steekproefgrootte 10

res %>%
  filter(n == 10) %>%
  select(mean,median) %>%
  gather(type,estimate) %>%
  ggplot(aes(x = type,y = estimate)) +
  geom_boxplot() +
  geom_hline(yintercept = fem$DirectChol %>%
    log2 %>%
    mean) +
  ggtitle("10 personen")

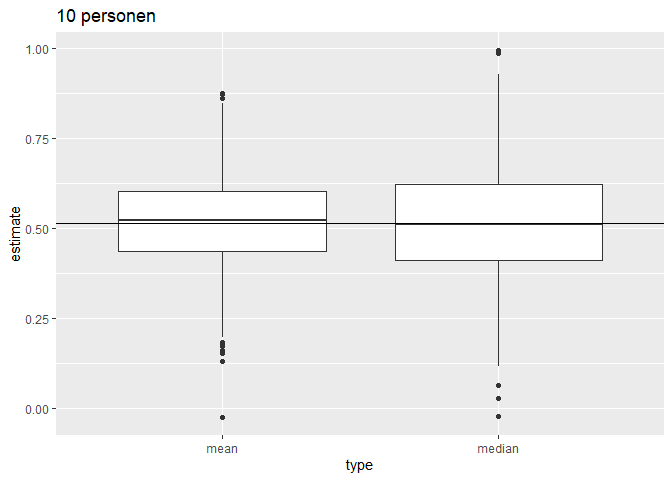
Vervolgens vergelijken we de verdeling van het gemiddelde en de mediaan in herhaalde steekproeven van steekproefgrootte 50.

res %>%
  filter(n == 50) %>%
  select(mean, median) %>%
  gather(type, estimate) %>%
  ggplot(aes(x = type,y = estimate)) +
  geom_boxplot()+
  geom_hline(yintercept = fem$DirectChol %>%
    log2 %>%
    mean) +
  ggtitle("50 personen")