A Nonogram is a Japanese picture puzzle in which a hidden picture can be found. This image can be formed by colouring the boxes of a rectangular lattice black or white, taking into account the set of integers that is specified for each row and each column of the grid. These numbers indicate how many consecutive black squares there should be in that row or column. For example, if the grid indicates the series 4 8 3 , this means that the row or column is made up of sets of four, eight, and three consecutive black boxes, in that order, and that there is at least one white box between each of the consecutive series.

Assignment

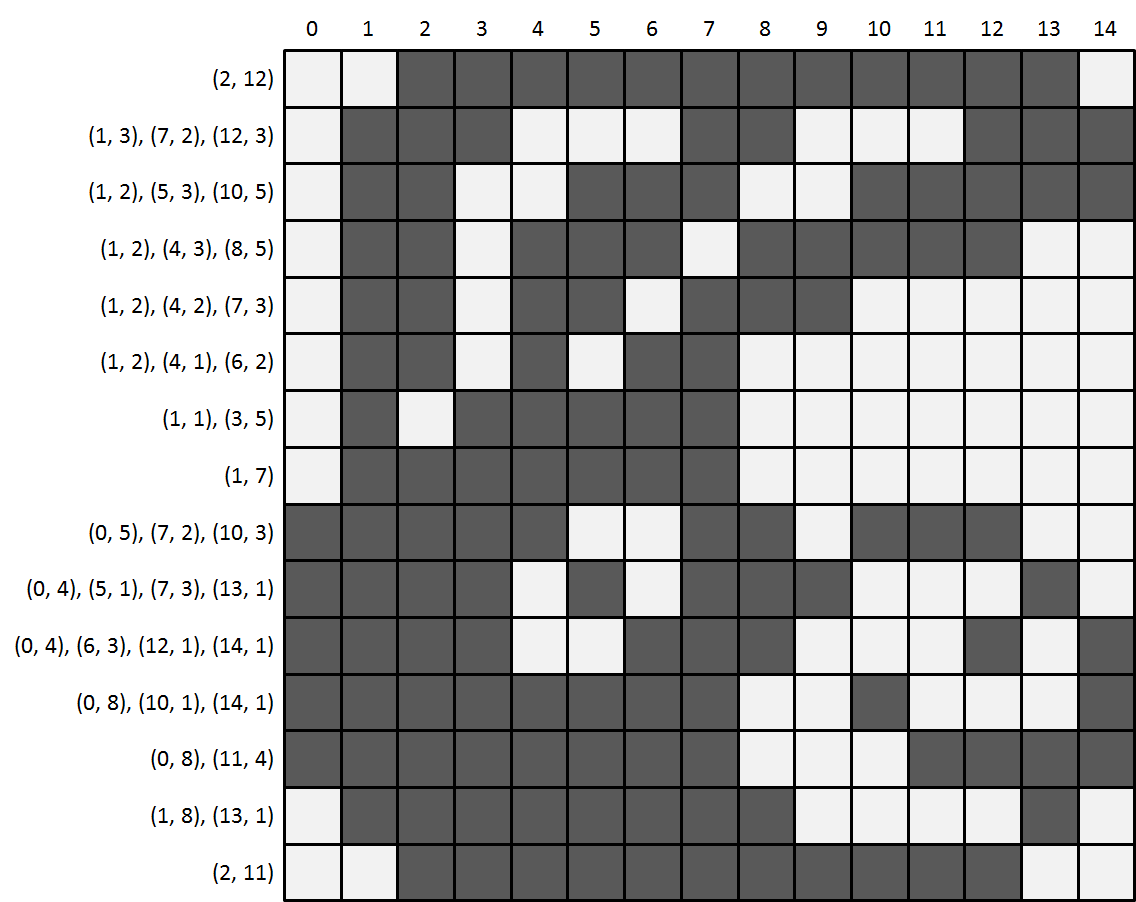
For this task, you must solve a simplified version of the Nonogram puzzle. As with the original puzzle, the sequences of black boxes in each row are provided. The description for the columns, however, is no longer needed. For each set of consecutive black boxes is now defined by a couple of integers $$(s, l)$$, where $$s$$ and $$l$$ indicate the start position and the length of the series, respectively. The far-left cell of a row is at position zero.

Note that the order in which the sequences of consecutive black boxes are given no longer plays a role. A row of a Nonogram puzzle can thus be defined by a container (a list, tuple, collection, …) of tuples. Each of these tuples consist of two integers that indicate the start position and the length of the series, respectively, of the consecutive black boxes. Asked:

• Write a function width to which the description of a row of a Nonogram puzzle should be passed. The function is to return the minimum width of that row as a result. The minimum width is the minimum number of boxes that the sequence must have, so that all the boxes from the description can be made black.

• Write a function line to which the description of a row of a Nonogram puzzle should be passed. The function must return the string representation of this line, in which white boxes are represented by spaces and black boxes by hashes (#). The function has an optional second parameter to which the number of boxes on the row can be passed. If no value is passed to this parameter, than the minimum width of the row is to be used as determined by the width function.

• Write a function nonogram to which the locations of two text files must be passed. The first text file contains a Nonogram puzzle. Each line of the file defines the corresponding line of the hidden image. This description consists of pairs of natural numbers: each couple consists of two integers, separated by a comma and enclosed in parentheses. The couples themselves are each separated by a semicolon. Except between the figures of the same natural number, spaces may furthermore occur on each spot within the description. The first and second number of each pair indicate the starting position and length, respectively, of a succession of black boxes on the line of the image.
  The function must write the hidden image which is described by the specifications of the Nonogram puzzle to a new text file, whose location was passed to the function as the second argument. Each line of the image must be generated by the function line, based on the corresponding description from the specifications of the puzzle. The width of the image is determined as the greatest possible minimum width of all rows that are defined in the specifications of the Nonogram puzzle.

Example

In the following example session we assume that the file stupid.puzzle.txt is in the current directory. Click on the name of the solution file to see the solution that was generated for the puzzle.

>>> width([(2, 12)])
14
>>> width(((1, 3), (7, 2), (12, 3)))
15
>>> width({(10, 5), (1, 2), (5, 3)})
15

>>> line([(2, 12)])
'  ############'
>>> line(((1, 3), (7, 2), (12, 3)), 20)
' ###   ##   ###     '
>>> line({(10, 5), (1, 2), (5, 3)})
' ##  ###  #####'

>>> nonogram('stupid.puzzle.txt', 'stupid.solution.txt')