In a classroom assignment, students are given a sequence of $$n$$ distinct integers and a sequence of $$n$$ boxes, with one inequality sign between each pair of consecutive boxes: less than (<) or greater than (>). That's $$n - 1$$ inequality signs in total. The challenge is to put the given integers in the boxes so that all inequalities between any two consecutive integers are satisfied.

In this classroom assignment, the students are given a sequence of $$n$$ distinct integers and a sequence of $$n$$ boxes, with one inequality sign between each pair of consecutive boxes: less than (<) or greater than (>). That's $$n - 1$$ inequality signs in total. The challenge is to put the given numbers in the boxes so that all inequalities between any two consecutive numbers are satisfied.

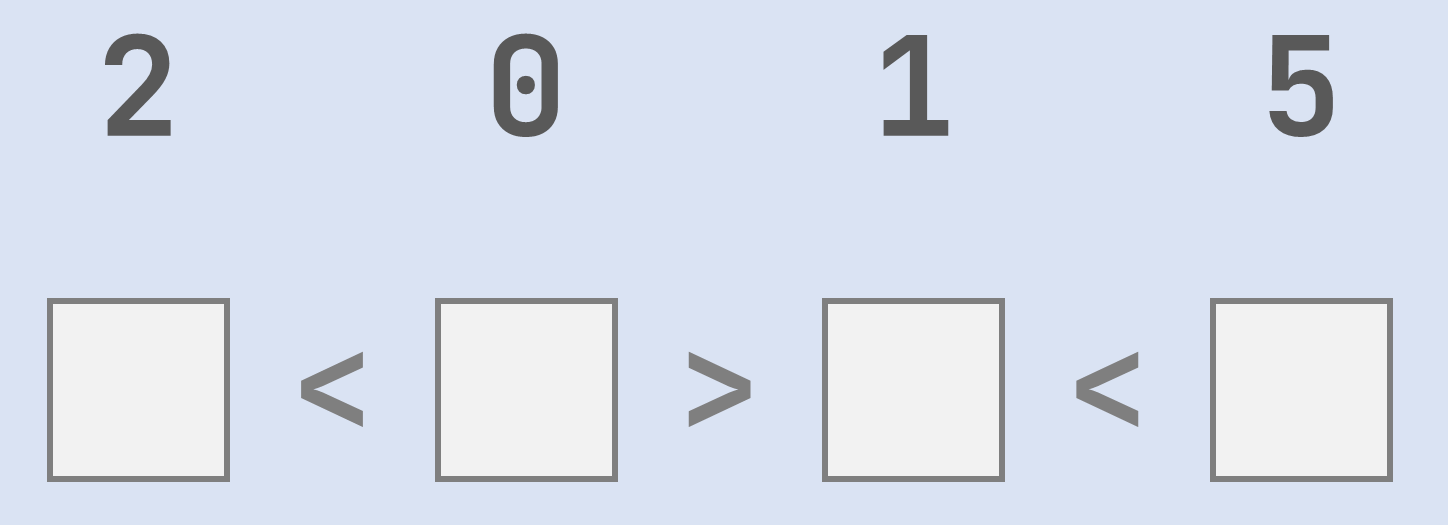
Simply putting the integers in the boxes in their given order will not always yield a correct solution. For instance, if we apply this strategy for the example assignment, then the first inequality is not satisfied, but the other two are.

Simply putting the numbers in the boxes in their given order does not yield a correct solution. The first inequality is not satisfied, but the other two are.

However, there is a simple trick to correctly fill in the given integers in the boxes. Start by sorting the integers in increasing order. Then process the inequality signs in reading order. If the next sign is a "less than"-sign (<), put the first (smallest) integer of the ranking in the box before the inequality sign. Otherwise, put the last (largest) integer of the ranking in that box. The integer that was put in the box is discarded from the ranking. After all inequality signs have been processed, put the only remaining integer in the ranking in the last box (to the far right).

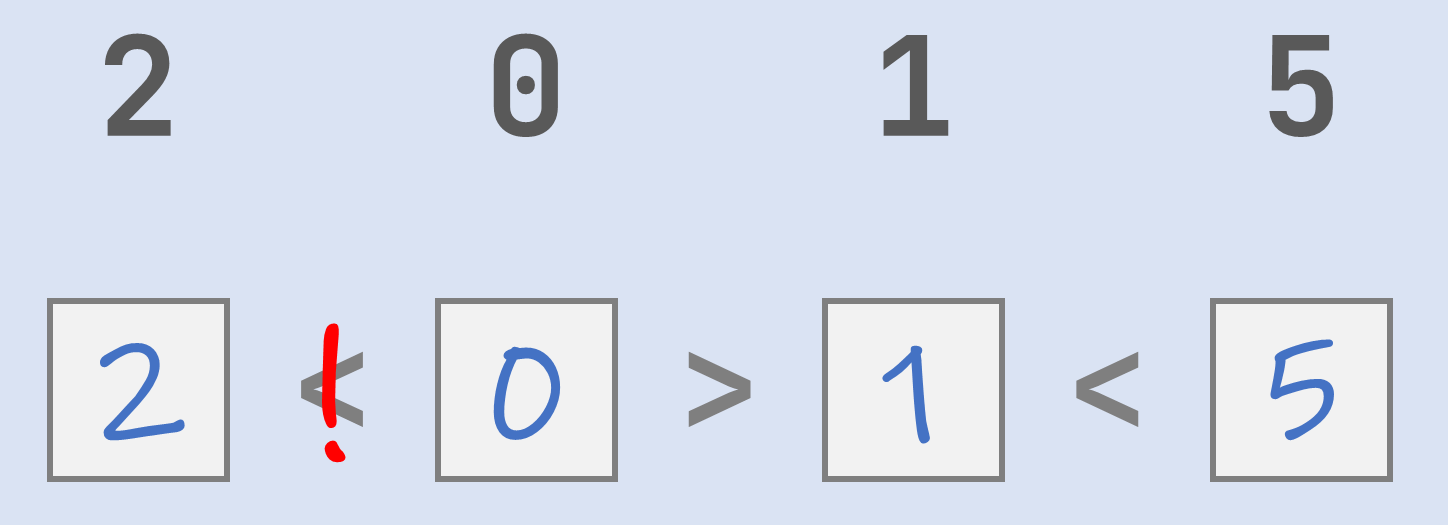
If this trick is applied to the example assignment, we start by sorting the integers in increasing order: 0 1 2 5. Going through the inequality signs from left to right, we first encounter a "less than"-sign (<). So we discard the leading 0 from the ranking and put it in the first box. The ranking that remains is 1 2 5. Then we come across a "greater than"-sign (>) and so we put the trailing 5 from the ranking in the second box. We also discard the trailing 5 from the ranking, leaving us with 1 2. The last inequality sign we encounter is a "less than"-sign (<), so we discard the trailing 1 from the ranking and put it in the third box. After this, only a 2 remains in the ranking, which we put in the last box. This results in the following sequence of inequalities that are all satisfied:

To find a correct placement, we start by sorting the numbers in increasing order: 0 1 2 5. If we then process the inequality signs from left to right, we first encounter a less than sign (<). So we discard the leading 0 from the ranking and put it in the first box. The ranking that remains is 1 2 5. Then we come across a greater than sign (>) and so we put the trailing 5 from the ranking in the second box. We also discard the trailing 5 from the ranking, leaving us with 1 2. The last inequality sign we encounter is less than (<), so we discard the trailing 1 from the ranking and put it in the third box. After this, only a 2 remains in the ranking, which we put in the last box. The result is a sequence of inequalities that are all satisfied.

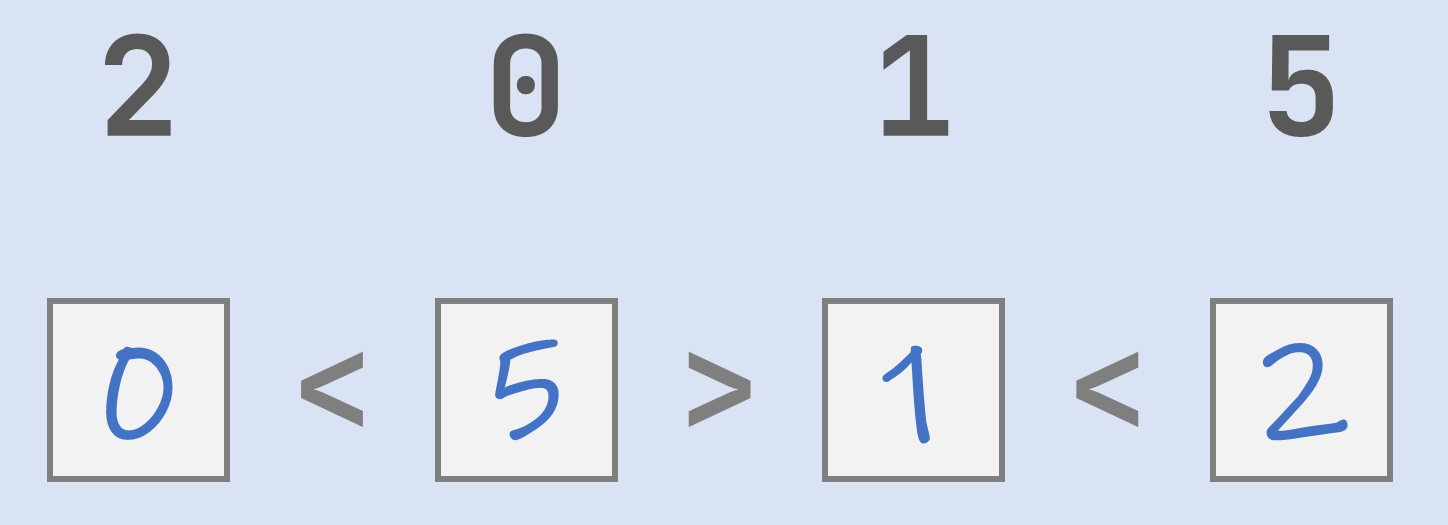
Now, this wouldn't be a typical classroom assignment, if it weren't for some student who didn't properly hear or read the assignment. For instance, the following solution was submitted by a student who left the integers in their original order, but rather rearranged the inequality signs instead of rearranging the integers.

In this case, some student left the numbers in their original order, but rather rearranged the inequality signs instead of rearranging the numbers. This also yields a sequence of inequalities that are all satisfied, but of course it was not the goal to solve the assignment in this way. After all, in some cases it is simply impossible to rearrange the given inequality signs so that all inequalities are satisfied.

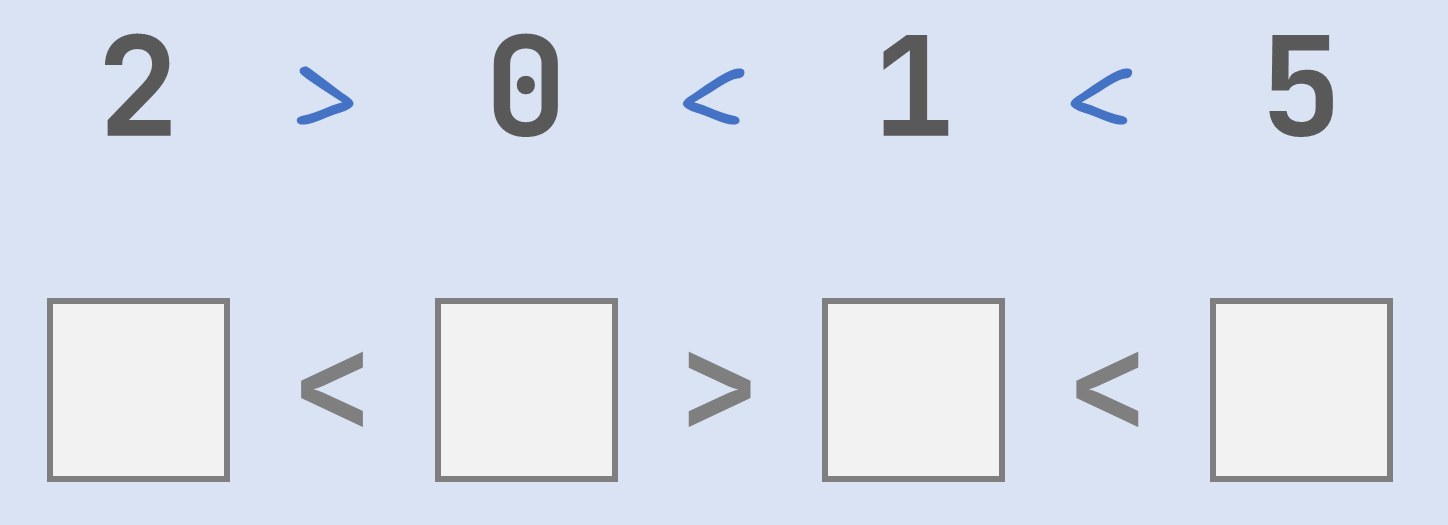
This also yields a sequence of inequalities that are all satisfied, but of course it was not the goal to solve the assignment in this way. After all, in some cases it is simply impossible to rearrange the given inequality signs so that all inequalities are satisfied.

Assignment

For an assignment as the one in the introduction, we represent the given integers as a list with $$n$$ integers (int). The given inequality signs are represented as a string (str) with $$n - 1$$ inequality signs: less than (<) or greater than (>). A possible solution for an assignment is also represented as a list with $$n$$ integers (int). Your task:

Write a function issatisfied that takes three arguments: i) an integer $$a$$ (int), ii) an inequality sign $$ \otimes $$ (str): less than (<) or greater than (>), and iii) an integer $$b$$. The function must return a Boolean value (bool) that indicates whether the inequality $$a \otimes b$$ is satisfied.
Write a function correct_signs that takes the given integers of an assignment. The function must return the inequality signs (str) that must be put in between the integers, so that all inequalities between any two consecutive integers are satisfied.
Write a function iscorrect that takes the given integers and the given inequality signs of an assignment. The function must return a Boolean value (bool) that indicates if putting the integers in the boxes in their given order yields a correct solution for the assignment.
Write a function number_placement that takes the given integers and the given inequality signs of an assignment. The function must return the correct solution for the assignment that is obtained by applying the trick from the introduction to put the integers in the boxes.
Write a function sign_placement that takes the given integers and the given inequality signs of an assignment. The function must return the rearrangement of the given inequality signs that will satisfy all inequalities between any two consecutive integers, if we put the rearranged inequality signs between the given integers one by one (without changing the order of the integers). If such a rearrangement does not exist, the function must raise an AssertionError with the message impossible placement.
Write a function assessment that takes a possible solution and the given inequality signs of an assignment. The function must return a string (str) that contains the integers of the given solution, in the given order. Each pair of successive integers is separated by a space, the next inequality sign and another space. For inequalities that are not satisfied, the inequality sign must be preceded by an exclamation mark (!), so < becomes !< and > becomes !>.

Example

        >>> issatisfied(13, '<', 42)
True
>>> issatisfied(13, '>', 42)
False

>>> correct_signs([2, 0, 1, 5])
'><<'
>>> correct_signs([0, 5, 1, 2])
'<><'

>>> iscorrect([2, 0, 1, 5], '<><')
False
>>> iscorrect([0, 5, 1, 2], '<><')
True

>>> number_placement([2, 0, 1, 5], '<><')
[0, 5, 1, 2]
>>> number_placement([66, 95, 6, 7, 73, 97, 69, 68, 51, 21, 3, 93, 58, 42, 54, 19], '<>>>>>><>><<><<')
[3, 97, 95, 93, 73, 69, 68, 6, 66, 58, 7, 19, 54, 21, 42, 51]

>>> sign_placement([2, 0, 1, 5], '<><')
'><<'
>>> sign_placement([66, 95, 6, 7, 73, 97, 69, 68, 51, 21, 3, 93, 58, 42, 54, 19], '<>>>>>><>><<><<')
'<><<<>>>>><>><>'
>>> sign_placement([82, 51, 5, 27, 19, 30, 26, 28, 12, 22], '<<>><><<>')
Traceback (most recent call last):
AssertionError: impossible placement

>>> assessment([2, 0, 1, 5], '<><')
'2 !< 0 !> 1 < 5'
>>> assessment([0, 5, 1, 2], '<><')
'0 < 5 > 1 < 2'
>>> assessment([66, 95, 6, 7, 73, 97, 69, 68, 51, 21, 3, 93, 58, 42, 54, 19], '<>>>>>><>><<><<')
'66 < 95 > 6 !> 7 !> 73 !> 97 > 69 > 68 !< 51 > 21 > 3 < 93 !< 58 > 42 < 54 !< 19'
>>> assessment([3, 97, 95, 93, 73, 69, 68, 6, 66, 58, 7, 19, 54, 21, 42, 51], '<>>>>>><>><<><<')
'3 < 97 > 95 > 93 > 73 > 69 > 68 > 6 < 66 > 58 > 7 < 19 < 54 > 21 < 42 < 51'

Assignment

Example

Epilogue