Kwadratensommen en Anova

Net zoals bij enkelvoudige regressie (Sectie 6.9) kunnen we opnieuw de kwadratensom van de regressie gebruiken bij het opstellen van de F-test. De kwadratensom van de regressie

$\begin{eqnarray*} \text{SSR}&=&\sum\limits_{i=1}^n (\hat Y_{i} -\bar Y)^2 \end{eqnarray*}$ kan nu worden herschreven als $\begin{eqnarray*} \text{SSR}&=&\sum\limits_{i=1}^n (\hat Y_i -\bar Y)^2\\ &=& \sum\limits_{i=1}^n (\hat{g} (x_{i1},x_{i2}) - \bar Y)^2\\ &=& \sum\limits_{i=1}^n (\hat\beta_0+\hat\beta_1x_{i1}+\hat\beta_2x_{i2}) - \bar Y)^2\\ &=& \sum\limits_{i=1}^{n_1} (\hat\beta_0 - \bar Y)^2 +\sum\limits_{i=1}^{n_2} (\hat\beta_0 + \hat\beta_1 - \bar Y)^2+\sum\limits_{i=1}^{n_3} (\hat\beta_0 + \hat\beta_2 - \bar Y)^2\\ &=& \sum\limits_{i=1}^{n_1} (\bar Y_1- \bar Y)^2 +\sum\limits_{i=1}^{n_2} (\bar Y_2- \bar Y)^2+\sum\limits_{i=1}^{n_3} (\bar Y_3 - \bar Y)^2\\ \end{eqnarray*}$

met $n_1$, $n_2$ en $n_3$ het aantal observaties in elke groep ($n-1=n_2=n_3=12$).

Net als in Sectie 6.9 is SSR een maat voor de afwijking tussen de predicties van het anova model (groepsgemiddelden) en het steekproefgemiddelde van de uitkomsten. Het kan opnieuw geïnterpreteerd worden als een maat voor de afwijking tussen het geschatte Model (3) en een gereduceerd model met enkel een intercept. Deze laatste is dus eigenlijk een schatting van het model $g(x_1,x_2)=\beta_0$, waarin $\beta_0$ geschat wordt door $\bar{Y}$. Anders geformuleerd: SSR meet de grootte van het behandelingseffect zodat $\text{SSR} \approx 0$ duidt op de afwezigheid van het effect van de dummy variabelen en $\text{SSR}>0$ duidt op een effect van de dummy variabelen. We voelen opnieuw aan dat $\text{SSR}$ zal kunnen worden gebruikt voor het ontwikkelen van een statistische test voor de evaluatie van het behandelingseffect. In de anova context heeft SSR $g-1=3-1=2$ vrijheidsgraden: de kwadratensom is opgebouwd op basis van $g=3$ groepsgemiddelden $\bar Y_j$ en we verliezen 1 vrijheidsgraad door de schatting van het algemeen steekproefgemiddelde $\bar Y$. Wanneer we SSR interpreteren als een verschil tussen twee modellen, bekomen we eveneens een verschil van $g-1=2$ vrijheidsgraden: $g=3$ model parameters in het volledige model (intercept voor referentie klasse en g-1 parameters voor elk van de dummies) en 1 parameter voor het gereduceerde model (enkel intercept).

In een ANOVA setting is het gebruikelijk om de kwadratensom van de regressie te noteren als $\text{SST}$, de kwadratensom van de behandeling (treatment) of als SSBetween. De kwadratensom van de behandeling geeft inderdaad de variabiliteit weer tussen de groepen. Het meet immers de afwijkingen tussen de groepsgemiddelden $\bar Y_j$ en het steekproefgemiddelde $\bar Y$ (Zie Figuur 44). We kunnen eveneens opnieuw een overeenkomstige gemiddelde kwadratensom bekomen als

\[\text{MST}=\text{SST}/(g-1).\]

met het aantal groepen $g=3$.

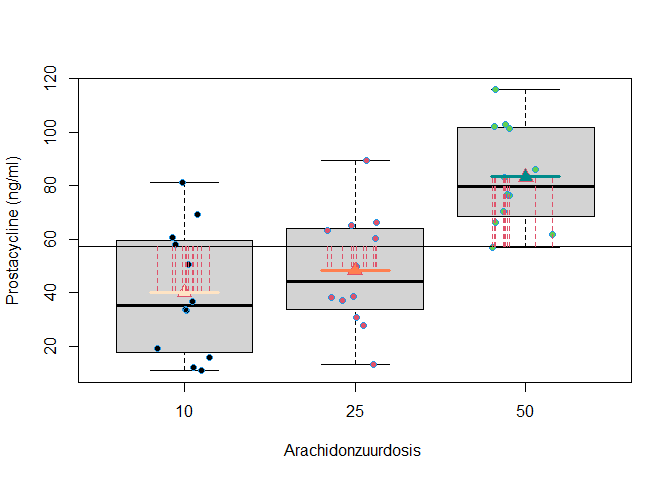
Figuur 44: Interpretatie van de kwadratensom van de behandeling (SST): de som van de kwadratische afwijkingen tussen de groepsgemiddelden ($$\bar Y_j$$) en het steekproefgemiddelde van de uitkomsten ($$\bar Y$$)

Opnieuw kunnen we de totale kwadratensom SSTot ontbinden in

\[\text{SSTot} = \text{SST} + \text{SSE}.\]

Waarbij SSTot opnieuw de totale variabiliteit voorstelt, met name de som van de kwadratische afwijking van de uitkomsten $Y_{i}$ t.o.v. het algemeen gemiddelde prostacycline niveau $\bar{Y}$ en SSE de residuele variabiliteit of de som van de kwadratische afwijkingen tussen de observaties $Y_{i}$ en de modelvoorspellingen (hier groepsgemiddelden) $\hat{g}(x_{i1},x_{i2})=\hat \mu_j=\bar Y_j$.

De interpretatie van de deze kwadratensommen worden weergegeven in Figuur 45.

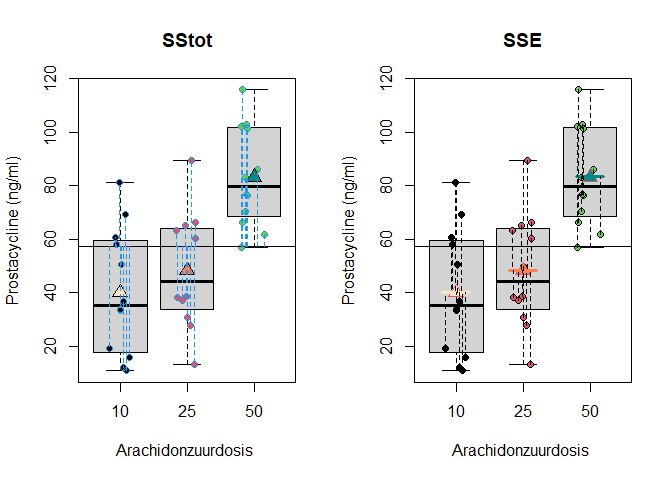
Figuur 45: Interpretatie van de totale kwadratensom (SSTot, som van de kwadratische afwijkingen tussen de uitkomsten $$Y_{i}$$ en het steekproefgemiddelde van de uitkomsten $$\bar Y$$, links) en van residuele kwadratensom (SSE, som van de kwadratische afwijkingen tussen de uitkomsten $$Y_{i}$$ en de groepsgemiddelden $$\bar Y_j$$, rechts)

Anova-test

Het testen van $H_0: \beta_1=\ldots=\beta_{g-1}=0$ vs $H_1: \exists k \in\{1,\ldots,g-1\} : \beta_k \neq0$ kan d.m.v. onderstaande $F$-test.

\[F = \frac{\text{MST}}{\text{MSE}}\]

met $\text{MST}$ de gemiddelde kwadratensom van de behandeling met $g-1$ vrijheidsgraden en $\text{MSE}$ de gemiddelde residuele kwadratensom uit het niet-gereduceerde model (3), deze heeft $n-g$ vrijheidsgraden (met het aantal groepen $g=3$). De teststatistiek vergelijkt dus variabiliteit verklaard door het model (MST) met de residuele variabiliteit (MSE) of met andere woorden vergelijkt het de variabiliteit tussen groepen (MST) met de variabiliteit binnen groepen (MSE). Grotere waarden voor de test-statistiek zijn minder waarschijnlijk onder de nulhypothese. Wanneer aan alle modelvoorwaarden is voldaan, dan volgt de statistiek onder de nulhypothese opnieuw een F-verdeling, $F \sim F_{g-1,n-g}$, met $g-1$ vrijheidsgraden in de teller en $n-g$ vrijheidsgraden in de noemer.

Anova Tabel

De kwadratensommen en de F-test worden meestal in een zogenaamde variantie-analyse tabel of een anova tabel gerapporteerd.

	Df	Sum Sq	Mean Sq	F value	Pr(\>F)
Treatment	vrijheidsgraden SST	SST	MST	f-statiestiek	p-waarde
Error	vrijheidsgraden SSE	SSE	MSE

De anovatabel voor het prostacycline voorbeeld kan als volgt in de R-software worden bekomen

anova(model1)

## Analysis of Variance Table
## 
## Response: prostac
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## dose       2  12658  6329.0  13.944 4.081e-05 ***
## Residuals 33  14979   453.9                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We kunnen dus opnieuw besluiten dat er een extreem significant effect is van de dosering van arachidonzuur op de gemiddelde prostacycline concentratie in het bloed bij ratten ($p<<0.001$).

In Figuur 46 wordt de F-verdeling weergegeven samen met de kritische waarde op het 5% significantie niveau en de geobserveerde F-statistiek voor het prostacycline voorbeeld.

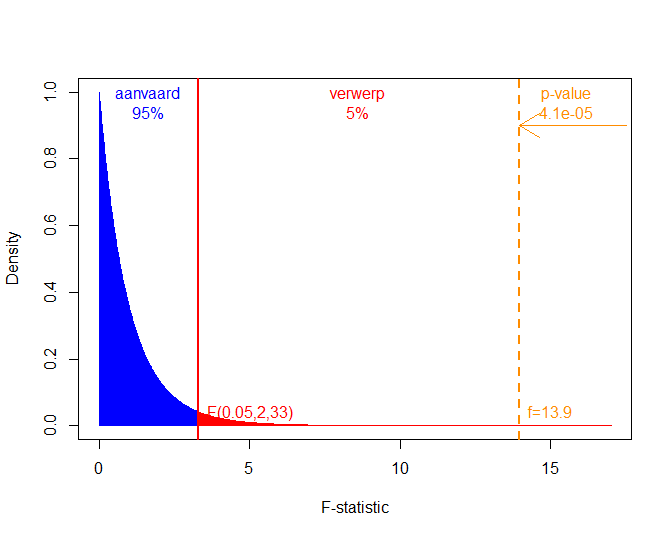
Figuur 46: Een F-verdeling met 2 vrijheidsgraden in de teller en 33 in de noemer. Het aanvaardingsgebied wordt weergegeven in blauw, de kritische waarde en de verwerpingsregio bij het $$\alpha=5\%$$ niveau in rood, en, de geobserveerde f-waarde en de p-waarde worden in oranje.

Voorbeelden van meerdere F-verdelingen met een verschillend aantal vrijheidsgraden in teller en noemer worden weergegeven in Figuur 47.

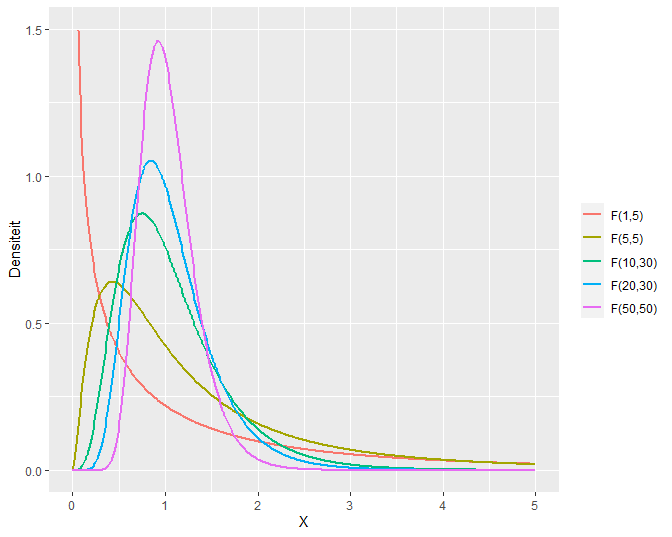
Figuur 47: Meerdere F-verdelingen met een verschillend aantal vrijheidsgraden in de teller en de noemer.