What's unusual about the number 313,340,350,000,000,000,499? Its English name
THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE
has the following letter count distribution:
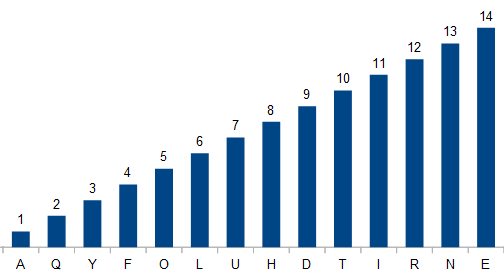
This makes the name a perfect "snowball" in the language of wordplay enthusiasts. This is a distribution where one letter occurs exactly once, one letter occurs exactly twice, one letter occurs exactly three times, and so on.
In exploring this phenomenon for the November 2012 issue of Word Ways, Eric Harshbarger and Mike Keith found hundreds of thousands of solutions among very large numbers. However, they note the following about the above example:
It is shockingly small compared to all other known snowball histogram numbers (of any order). It seems very likely that this is the smallest snowball histogram number of any order, but a proof of this fact, even with computer assistance, seems difficult.
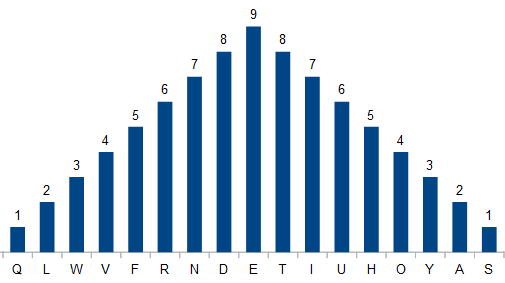
In the same article, Harshbarger and Keith come up with two other pretty findings. The number 224,000,000,000,525,535, or
TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE
produces a "growing/melting" snowball:
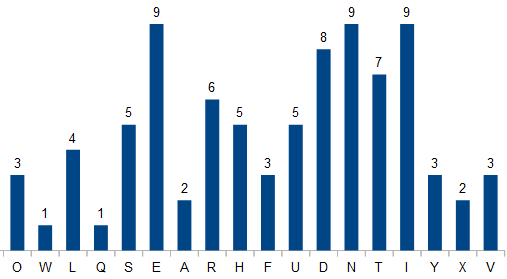
And the number 520,636,000,000,757,000, or
FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND
has a letter count distribution that corresponds to the first 18 digits of the constant $$\pi$$:
At the end of their article they make the following consideration:
This idea can also be applied to arbitrary text, not just number names. Can you find a sentence in Moby Dick or Pride and Prejudice whose letter distribution is a snowball or is interesting in some other way? Such possibilities are left for future consideration.
Assignment
In this assignment, we represent the letter count distribution of a given string as a dictionary that maps all letters that occur in the string onto their number of occurrences in the string. Letter counting is done case insensitive, where the uppercase version of the letters are used as keys in the dictionary. Letters that do not occur in the string should not be used as keys in the dictionary. The characters of the string that are not letters should be ignored when determining the letter count distribution. Your task:
-
Write a function letter_distribution that takes a string argument. The function must return a dictionary that represents the letter count distribution of the given string.
-
Write a function snowball that takes a string argument. The function must return a Boolean value that indicates whether the letter count distribution of the given string corresponds to a snowball distribution.
-
Write a function pyramid that takes a string argument. The function must return a Boolean value that indicates whether the letter count distribution of the given string corresponds to a "growing/melting" snowball distribution.
Clarification
If the number of different letters that occur in the given string is even, the two middle letters of the pyramid have the same number of occurrences. As a result, the pyramid has as a smoothed top in that case.
-
Write a function pi that takes a string argument. The function must return a Boolean value that indicates whether the letter count distribution of the given string corresponds to the first digits of the number $$\pi$$.
Tip
Before you start looking for an accurate representation of the number $$\pi$$, here are its first 50 significant digits:
3.1415926535897932384626433832795028841971693993751
Example
>>> letter_distribution('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
{'U': 7, 'I': 11, 'T': 10, 'L': 6, 'O': 5, 'Q': 2, 'N': 13, 'E': 14, 'D': 9, 'A': 1, 'R': 12, 'F': 4, 'H': 8, 'Y': 3}
>>> letter_distribution('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
{'W': 3, 'V': 4, 'U': 6, 'I': 7, 'T': 8, 'A': 2, 'O': 4, 'Q': 1, 'N': 7, 'E': 9, 'D': 8, 'R': 6, 'S': 1, 'F': 5, 'H': 5, 'Y': 3, 'L': 2}
>>> letter_distribution('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
{'W': 1, 'X': 2, 'V': 3, 'U': 5, 'I': 9, 'T': 7, 'A': 2, 'O': 3, 'Q': 1, 'N': 9, 'E': 9, 'D': 8, 'R': 6, 'S': 5, 'F': 3, 'H': 5, 'Y': 3, 'L': 4}
>>> snowball('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
True
>>> snowball('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
False
>>> snowball('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
False
>>> pyramid('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
False
>>> pyramid('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
True
>>> pyramid('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
False
>>> pi('THREE HUNDRED THIRTEEN QUINTILLION THREE HUNDRED FORTY QUADRILLION THREE HUNDRED FIFTY TRILLION FOUR HUNDRED NINETY-NINE')
False
>>> pi('TWO HUNDRED TWENTY-FOUR QUADRILLION FIVE HUNDRED TWENTY-FIVE THOUSAND FIVE HUNDRED THIRTY-FIVE')
False
>>> pi('FIVE HUNDRED TWENTY QUADRILLION SIX HUNDRED THIRTY-SIX TRILLION SEVEN HUNDRED FIFTY-SEVEN THOUSAND')
True