Een minimaal opspannende boom¹ (minimal spanning tree MST), is een graaf waarbij alle knopen met elkaar verbonden zijn, met een minimaal gewicht.

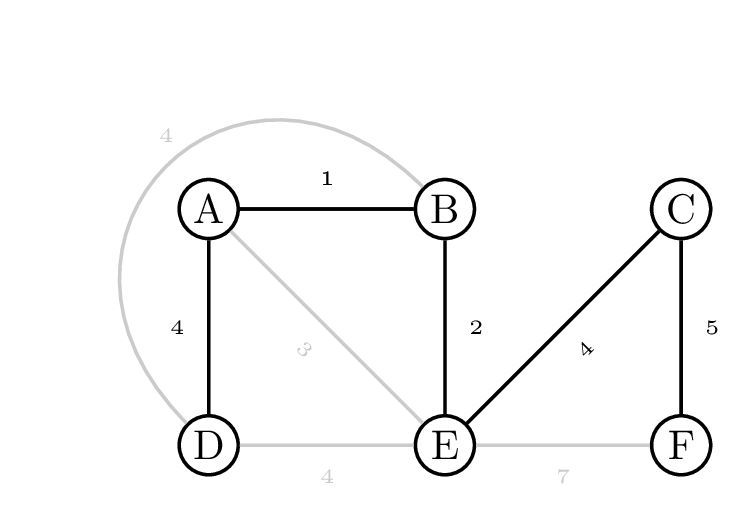
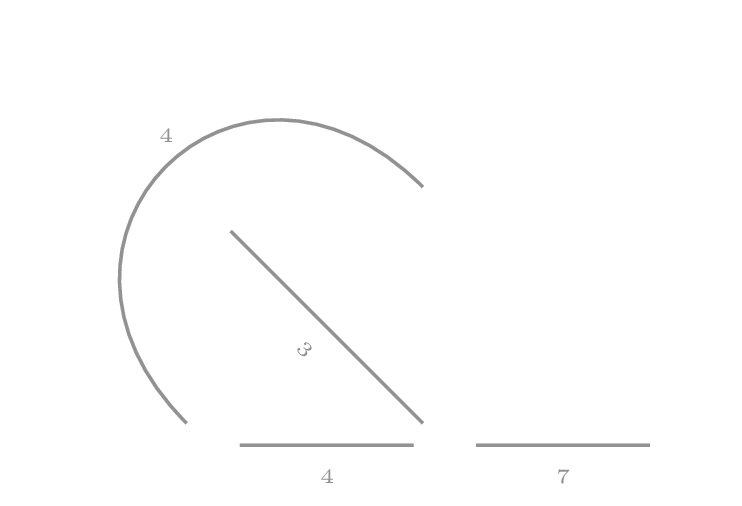
Hier zie je een voorbeeld van een minimaal opspannende boom binnen een graaf. Het is mogelijk om van elke knoop naar elke andere knoop te wandelen en hierbij is de totale som van de bogen minimaal.

Er zijn verschillende manieren om gegeven een graaf een minimaal opspannende boom op te stellen. Eén van de mogelijkheden is het algoritme van van Prim². In 1930 door de Tsjechische wiskundige Vojtěch Jarník ontdekt, daarna verloren gegaan en later herontdekt door de informaticus Robert C. Prim.

Het algoritme werkt door de minimaal opspannende boom (MST) stapsgewijs op te bouwen.

• Kies een willekeurige startknoop \(v_1\).
• Analyseer alle bogen die verbonden zijn met \(v_1\) en voeg de boog met minimaal gewicht toe aan de MST.
• De minimaal opspannende boom bestaat nu uit één enkele boog.
  • Beschouw nu alle toppen die verbonden kunnen worden met de huidige MST en de bijbehorende bogen.
  • Voeg opnieuw de boog met minimaal gewicht toe aan de MST.
• Herhaal dit proces tot het aantal bogen in de MST gelijk is aan \(n-1\), met \(n\) het aantal toppen.

Opgave

Schrijf een functie MST_prim( V, E ) waarbij V een lijst met toppen voorstelt en E een lijst opgesteld uit tupels van bogen met hun gewicht. Kies als startwaarde steeds de eerste knoop die voorkomt in V. Met andere woorden, stel v1 = V[0].

Voorbeelden

>>> MST_prim( ['A', 'B', 'C', 'D', 'E'], 
              [('A', 'B', 3), ('B', 'C', 4),('C', 'D', 2),('B', 'D', 7),('B', 'E', 8)] )
[('A', 'B', 3), ('B', 'C', 4), ('C', 'D', 2), ('B', 'E', 8)]

>>> MST_prim( ['A', 'B', 'C', 'D', 'E', 'F', 'G'],
              [('A','D',5), ('A', 'B', 7), ('B','D',9), ('B','C',8), ('C','E',5), ('B','E',7), 
               ('D','E',15), ('D','F',6), ('F', 'E', 8), ('E', 'G',9), ('F','G',11)] ) 
[('A', 'D', 5), ('D', 'F', 6), ('A', 'B', 7), ('B', 'E', 7), ('C', 'E', 5), ('E', 'G', 9)]