Opgave

Je beschikt over een heuse boekencollectie en wenst deze zo efficiënt mogelijk te organiseren.
Online vind je een boekenrekkenwinkel met een bizarre promotie: alle rekken worden tegen dezelfde lage prijs verkocht. De enige adder onder het gras is dat de rekken in grootte verschillen, maar gezien je krap bij kas zit, ben je bereid dit door de vingers te zien.

Een boek wordt gekenmerkt door een titel en een dikte uitgedrukt in millimeter. Een boekenrek heeft een bepaalde breedte. Deze breedte bepaalt hoeveel boeken op een rek passen: de som van de boekdiktes mag de rekbreedte niet overschrijden.



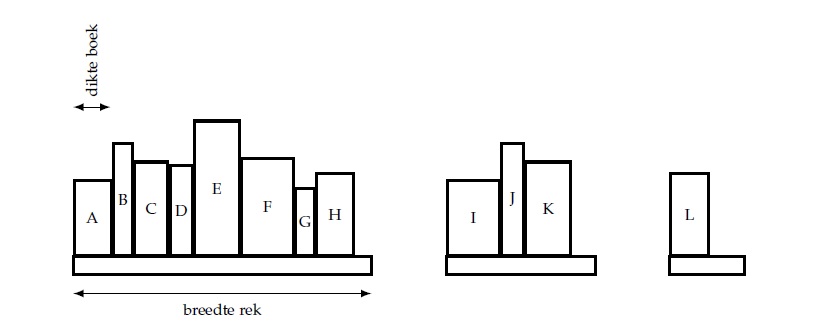
Je gaat als volgt te werk: eerst sorteer je je boeken alfabetisch. Je neemt vervolgens het breedste rek en je plaatst er zoveel mogelijk boeken op (in alfabetische volgorde). Indien niet alle boeken erop passen, neem je het tweede breedste rek en plaats je hierop de resterende boeken. Je blijft zo extra rekken bijnemen tot alle boeken een plaats hebben gekregen op een rek.
De vraag is dan: hoeveel rekken heb je in totaal nodig?

Mogelijk zijn er onvoldoende rekken om al je boeken in alfabetische volgorde op kwijt te kunnen. Stel bijvoorbeeld dat de winkel twee rekken verkoopt: één van 8 cm en één van 3 cm. Je hebt twee boeken: “Acacia’s” van 2 cm dik en “Zonnebloemen” van 7 cm dik.
Je werkwijze gebiedt je te beginnen met het breedste rek van 8 cm en hierop “Acacia’s” te plaatsen. Je hebt dan nog maar 6 cm over, niet genoeg voor “Zonnebloemen”. Je schakelt over naar het volgende rek: enkel dat van 3 cm blijft over. Hier past “Zonnebloemen” ook niet op. Je concludeert hieruit dat het onmogelijk is je boeken naar wens te ordenen.

---

Invoer

De eerste regel bevat het aantal testgevallen. Per testgeval volgt:

• Een regel met door één spatie gescheiden gehele getallen. Het eerste gehele getal N weerspiegelt het aantal boekenrekken. De volgende N getallen B₁; B₂; : : : ; B_N stellen de breedtes voor van de boekenrekken. Hierbij zijn 0 ≤ N ≤ 100 en 0 < B_i ≤ 1000.
• Een regel met een enkel geheel getal n met 0 ≤ n ≤ 100. Dit stelt het aantal boeken voor.
• n regels die elk één boek beschrijven. Elke regel bevat achtereenvolgens:

            - één geheel getal D dat de dikte van een boek voorstelt;
            - één spatie;
            - de naam van het boek.

Voorbeeldinvoer:

2
4 150 150 150 150
5
70 A Game of Thrones
76 A Clash of Kings
99 A Storm of Swords
75 A Feast for Crows
105 A Dance With Dragons
3 500 500 500
3
1309 Artemene
303 A la recherche du temps perdu
399 Mission Earth

---

Uitvoer

Per testgeval dien je één regel uit te voeren. Deze regel bestaat uit:

• de index van het testgeval, beginnende bij 1;
• één spatie;
• het minimaal benodigde aantal boekenrekken of ONMOGELIJK indien er onvoldoende rekken zijn.

Voorbeelduitvoer:

1 4
2 ONMOGELIJK