The greater honeyguide (Indicator indicator) living in Africa is obsessed with beeswax, but is not always able to penetrate a hive on his own. Therefore, he has forged a unique partnership with man. The bird attracts the attention of local honey hunters with his rattling cry, flies in the direction of a beehive and regularly stops to cry again. When they reach the hive, the hunter breaks it open, intoxicates the bees with smoke, takes the honey out and leaves the wax for the bird.
This collaboration saves man an average of 5.7 hours of time to find beehives but it is not infallible. "The greater honeyguide has also brought us to the edge of an abyss and to a male elephant", reported biologists Lester Short and Jennifer Horne. "In those cases, there were beehives at the bottom of the cliff (in a valley) and behind the elephant. The welfare of the escorted persons is none of the greater honeyguide's concern."
Assignment
A group of biologists is mapping beehives in the Kenyan savanna, following the bird call of the greater honeyguide. If they have been guided to a hive, they indicate the location of the hive on a rectangular map. The map is divided into square areas. As shown in the example below, the rows of the map are labeled top to bottom with the uppercase letters A, B, …, and the columns from left to right with the numbers 1, 2, 3, …. The square areas are labeled with lowercase letters indicating the types of vegetation as landmarks in the savannah.
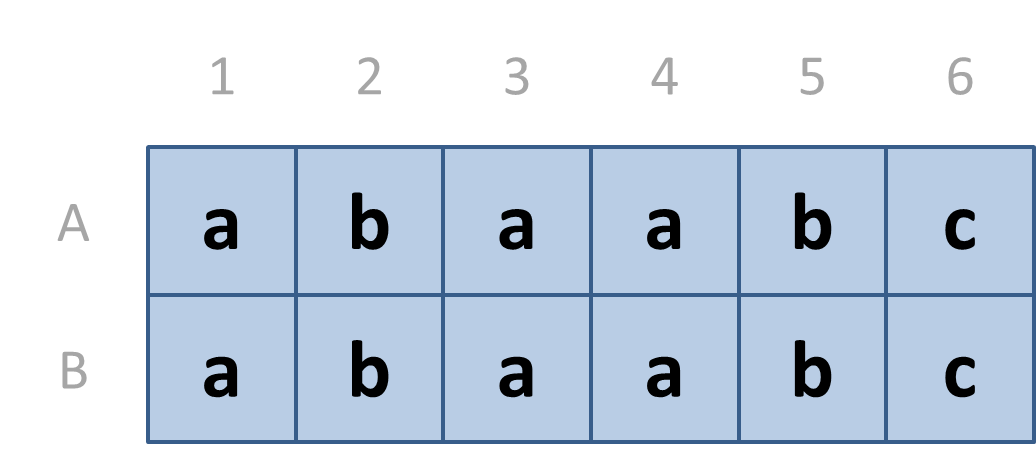
When the biologists find a hive with the help of the honeyguide, they have no idea of the position on the map where they left. Fortunately, they have a good sense of direction and can reconstruct the route they have traveled as a sequence of observations and movements.
A route can be described as a string (str) in which observations are indicated by lowercase letters that describe the type of vegetation and movements by uppercase letters that indicate the direction: L for left, R for right, U for up and D for down. Observations and movements always alternate in the description of the route, and the description always starts and ends with an observation. If the execution of a movement would lead to a square outside the map, the movement is not performed and one stays at the same position.
Your task is to find all possible positions on the map where a given route may end. These indicate the possible positions of the beehives. Suppose we need to find every position on the above map where we can end up when following the route bLaLa. The possible end positions, and the corresponding routes are shown in the figure below.
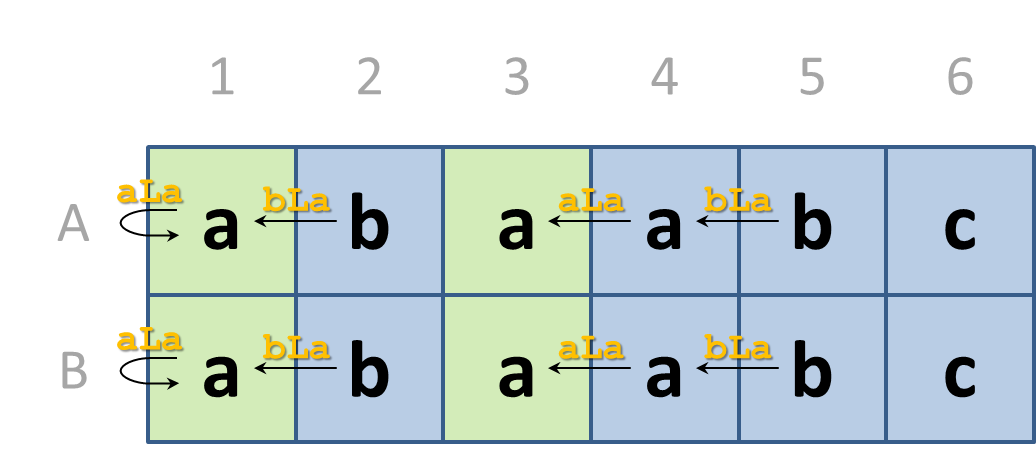
In columns 2 and 5 there is always a lowercase letter b, and therefore the route can start there. If we move to the left from the starting positions, then we always arrive at a square that is labeled with the letter a. So we can continue to follow the route. If we move to the left again, the routes that started at column 5 finish at a square in column 3. These position all have a letter a, so we have been following the route completely. The squares in column 3 are therefore possible end positions. The routes that started at column 2 end after one movement at column 1. If we were to move left again, we would drop outside the map. We therefore stay put, but end up at a square with the letter a. Again, in those cases we have been able to follow the route completely and the squares in column 1 are possible end positions.
The biologists indicate the position of a square on the map with a label (a string) which consists of the row label followed by the column label. In Python, however, it is customary to index rows top to bottom and columns left to right with integers, each time starting from zero. Therefore, first write the following two functions:
-
A function coord2label that returns the label (str) corresponding to the given row and column index (int; two separate arguments).
-
A function label2coord that returns the row (int) and column (int) indices (as a tuple) corresponding to the given label (str).
You may assume that the number of rows on the map never exceeds 26. Now, use the above functions to implement the following three functions.
-
Write a function observation that takes three arguments: i) the number (int) of rows in a rectangular map, ii) a string (str) of lowercase letters that indicate the labels of the squares on the map, read from left to right and from top to bottom, and iii) the label (str) of a square on the map. The function must return the lowercase letter (str) at the square of the map indicated by the given label.
-
Use the function observation to write a function endpoint that takes four arguments. The first three arguments are identical to the arguments passed to the function observation. The fourth argument is a string (str) containing directions. The label provides a starting point on the map. The function must return the label (str) of the end point on the map that is reached when the given route is followed completely. If it is not possible to follow the given route completely from the given starting point, the function must return the value None.
-
Use the function endpoint to write a function beehives that takes three arguments. The first two arguments are identical to the corresponding arguments passed to the functions observation and endpoint. The third argument is a string (str) containing directions. The function must return a list (list) containing the labels (str) that are possible end positions that can be reached if the given route is followed completely. The same label can appear at most once in this list, and the labels must be listed in lexicographical order.
Example
>>> coord2label(0, 0)
'A1'
>>> coord2label(1, 5)
'B6'
>>> coord2label(7, 4)
'H5'
>>> label2coord('A1')
(0, 0)
>>> label2coord('B6')
(1, 5)
>>> label2coord('H5')
(7, 4)
>>> observation(2, 'abaabcabaabc', 'A1')
'a'
>>> observation(2, 'abaabcabaabc', 'B6')
'c'
>>> endpoint(2, 'abaabcabaabc', 'A5', 'bLaLa')
'A3'
>>> endpoint(2, 'abcdeecdea', 'B4', 'eLdLcUb')
'A2'
>>> endpoint(2, 'abcdeecdea', 'A3', 'cRdUcLbLaDa')
>>> beehives(2, 'abaabcabaabc', 'bLaLa')
['A1', 'A3', 'B1', 'B3']
>>> beehives(2, 'abcdeecdea', 'eLdLcUb')
['A2']
>>> beehives(2, 'abcdeecdea', 'cRdUcLbLaDa')
[]Note that the possible routes leading to the four possible end points of the first example of the function beehives are depicted graphically in the introduction of this assignment.
Below, we show a representation of the rectangular map for the second example, with the row and column labels as used by the biologists. Labels of the squares that belong to a possible route are shown in black, and labels that do not belong to a route in gray. Labels that are possible a starting points of route are shown in blue, labels that are possible end points are shown in yellow, and labels that may both be a starting and end point are shown in green. This representation is also used as feedback for the test cases of the function beehives for which your submitted source code produces the wrong answer.
12345
A abcde
B ecdea