The pseudocode for SmallParsimony is shown below. It returns the parsimony score for a binary rooted tree $$T$$ whose leaves are labeled by symbols stored in an array Character (i.e., Character($$v$$) is the label of leaf $$v$$). At each iteration, it selects a node $$v$$ and computes $$s_k(v)$$ for each symbol $$k$$ in the alphabet. For each node $$v$$, SmallParsimony maintains a value Tag($$v$$), which indicates whether the node has been processed (i.e., Tag($$v$$) = 1 if the array $$s_k(v)$$ has been computed and Tag(v) = 0 otherwise). We call an internal node of $$T$$ ripe if its tag is 0 but its children's tags are both 1. SmallParsimony works upward from the leaves, finding a ripe node $$v$$ at which to compute $$s_k(v)$$ at each step.
SmallParsimony(T, Character) for each node v in tree T Tag(v) ← 0 if v is a leaf Tag(v) ← 1 for each symbol k in the alphabet if Character(v) = k sk(v) ← 0 else sk(v) ← ∞ while there exist ripe nodes in T v ← a ripe node in T Tag(v) ← 1 for each symbol k in the alphabet sk(v) ← minimum over all symbols i {si(Daughter(v)) + δi,k} + minimum over all symbols j {sj(Son(v)) + δj,k} return minimum over all symbols k {sk(v)}
Assignment
Rooted trees
Define a class Tree that can be used to represent edge-weighted rooted binary trees whose nodes are labeled and whose edges are weighted with a floating point number. The initialization method takes the following optional parameters:
-
label (object, default value: None): label of root node or None if root node is unlabeled
-
lt (Tree or NoneType, default value: None): left subtree or None if root node is a leaf node
-
lw (int or NoneType, default value: None): weight of edge connecting root note to its left subtree or None if root node is a leaf node or if edge connecting root node to left subtree is unweighted
-
rt (Tree or NoneType, default value: None): right subtree or None if root node is a leaf node
-
rw (int or NoneType, default value: None): weight of edge connecting root note to its right subtree or None if root node is a leaf node or if edge connecting root node to right subtree is unweighted
The class Tree must support at least the following methods:
-
A static or class method loadtxt that can be used to read a rooted binary tree from a text file. The method takes the file name or the file handle of the text file. The text file must contain a description of an rooted tree as an adjacency list. Each line contains the description of an edge $$(i, j)$$ in the tree: the unique label $$i$$ of a node higher in the tree (closer to the root node), the symbols -> and the unique label $$j$$ of a node deeper in the tree (further away from the root node). Node labels that contain only digits represent internal nodes of the tree must be converted to integers, otherwise the node labels considered as strings and correspond to leaf nodes. The method must return an object of the class Tree.
An equality implementation, __eq__, that can be used to check if two trees represent the same data. The order of the children matters.
Make sure the built-in function repr returns string representations of objects of the class Tree that are formatted according to the example given below: the label (if any) is not passed as a keyword argument, whereas all other arguments are passed as keyword arguments.
Small parsimony
Define a function small_parsimony that takes a rooted binary tree with $$n$$ leaves labeled by DNA string (Tree). The function must return the given tree (Tree) as an edge-weighted rooted binary tree, whose internal nodes have been labeled by DNA strings that minimize the parsimony score of the tree.
Note
Remember to run SmallParsimony on each individual index of the strings at the leaves of the tree.
Example
In the following example we assume the text file tree.txt1 to be located in the current directory.
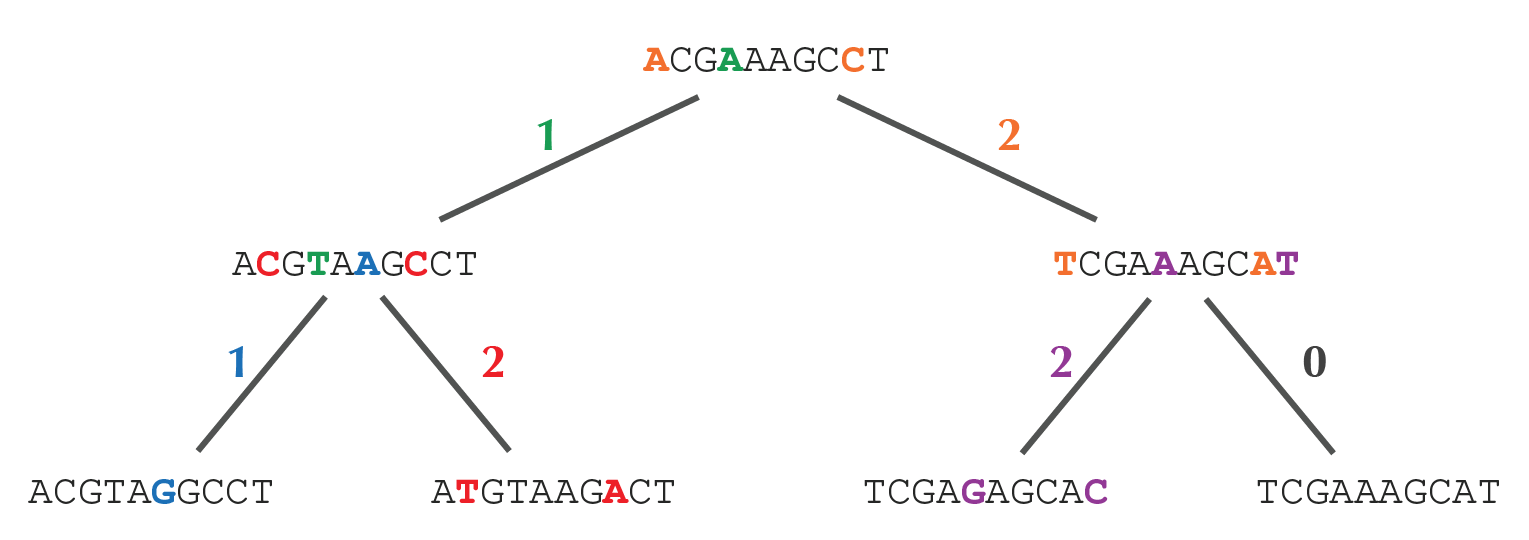
>>> Tree('label') Tree('label') >>> Tree() == Tree() True >>> Tree(0, lt=Tree(1), rt=Tree(2)) Tree(0, lt=Tree(1), rt=Tree(2)) >>> Tree(0, lt=Tree(1), lw=1, rt=Tree(2), rw=3) Tree(0, lt=Tree(1), lw=1, rt=Tree(2), rw=3) >>> tree = Tree.loadtxt('tree.txt2') >>> tree Tree(lt=Tree(lt=Tree('ACGTAGGCCT'), rt=Tree('ATGTAAGACT')), rt=Tree(lt=Tree('TCGAGAGCAC'), rt=Tree('TCGAAAGCAT'))) >>> small_parsimony(tree, 'ACGT') Tree('ACGAAAGCAT', lt=Tree('ACGTAAGCCT', lt=Tree('ACGTAGGCCT'), lw=1, rt=Tree('ATGTAAGACT'), rw=2), lw=2, rt=Tree('TCGAAAGCAT', lt=Tree('TCGAGAGCAC'), lw=2, rt=Tree('TCGAAAGCAT'), rw=0), rw=1)
Here's the rooted binary tree with minimal parsimony score 8 that corresponds to the tree in the above example.