What's unusual about these dice is obvious, but what's normal about them?

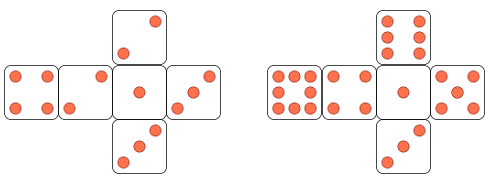
sicherman
Sicherman dice

These dice were discovered by George Sicherman (Buffalo, New York, USA) and were originally reported by Martin Gardner in a 1978 article in Scientific American. When the dice are thrown together, they produce the same probability distribution as a pair of ordinary dice. There are six ways to throw a 7, five ways to throw an 8, etc. Moreover, the Sicherman dice are the only possible alternate arrangement of strictly positive integers that result in the same probability distribution as a pair of ordinary dice.

It is a standard exercise in elementary combinatorics to calculate the number of ways of rolling any given value with a pair of fair six-sided dice (by taking the sum of the two rolls). The table shows the number of such ways of rolling a given value $$n$$:

$$n$$ 2 3 4 5 6 7 8 9 10 11 12
# of ways 1 2 3 4 5 6 5 4 3 2 1

A question arises whether there are other ways of relabeling the faces of the dice with positive integers that generate these sums with the same frequencies. The surprising answer to this question is that there does indeed exist such a way. These are the Sicherman dice. Three additional rearrangements having the same probability distribution as  a pair of ordinary dice are possible if the dice are allowed to have empty sides.

The table below lists all possible totals of dice rolls with standard dice and Sicherman dice. One Sicherman die is coloured for clarity 1–2–2–3–2–4 and the other is all black 1–3–4–5–6–8.


2 3 4 5 6 7 8 9 10 11 12
ordinary dice 1+1 1+2
2+1		 1+3
2+2
3+1		 1+4
2+3
3+2
4+1		 1+5
2+4
3+3
4+2
5+1		 1+6
2+5
3+4
4+3
5+2
6+1		 2+6
3+5
4+4
5+3
6+2		 3+6
4+5
5+4
6+3		 4+6
5+5
6+4		 5+6
6+5		 6+6
Sicherman dice 1+1 2+1
2+1		 3+1
3+1
1+3		 1+4
2+3
2+3
4+1		 1+5
2+4
2+4
3+3
3+3		 1+6
2+5
2+5
3+4
3+4
4+3		 2+6
2+6
3+5
3+5
4+4		 1+8
3+6
3+6
4+5		 2+8
2+8
4+6		 3+8
3+8		 4+8

Assignment

In this exercise, the outcome of a throw with a pair of dice is represented as a tuple $$(x, y)$$ where $$x \in \mathbb{N}$$ represents the number of pips at the top side of the first die, and $$y \in \mathbb{N}$$ the number of pips at the top side of the second die. Note that we do not limit ourselves in this exercise to six-sided dice, and that the a single die may have sides carrying the same number of pips. A pair of dice is represented a list or tuple of two dice. Your task:

Example

>>> dice6_1 = {1, 2, 3, 4, 5, 6}
>>> dice6_2 = [1, 2, 2, 3, 3, 4]
>>> dice6_3 = (1, 3, 4, 5, 6, 8)

>>> throw = combinations(dice6_1, dice6_1)
>>> throw[8]
[(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)]
>>> throw = combinations(dice6_2, dice6_3)
>>> throw[8]
[(2, 6), (2, 6), (3, 5), (3, 5), (4, 4)]

>>> distribution(dice6_1, dice6_1)
{2: 1, 3: 2, 4: 3, 5: 4, 6: 5, 7: 6, 8: 5, 9: 4, 10: 3, 11: 2, 12: 1}
>>> distribution(dice6_2, dice6_3)
{2: 1, 3: 2, 4: 3, 5: 4, 6: 5, 7: 6, 8: 5, 9: 4, 10: 3, 11: 2, 12: 1}

>>> equalDistribution([dice6_1, dice6_1], (dice6_2, dice6_3))
True

>>> dice8_1 = {1, 2, 3, 4, 5, 6, 7, 8}
>>> dice8_2 = (1, 3, 5, 5, 7, 7, 9, 11)
>>> dice8_3 = (1, 2, 2, 3, 3, 4, 4, 5)
>>> dice8_4 = (1, 2, 5, 5, 6, 6, 9, 10)
>>> dice8_5 = (1, 2, 3, 3, 4, 4, 5, 6)
>>> equalDistribution((dice8_1, dice8_1), (dice8_2, dice8_3))
True
>>> equalDistribution((dice8_1, dice8_1), (dice8_3, dice8_4))
False
>>> equalDistribution((dice8_1, dice8_1), (dice8_4, dice8_5))
True

Resources