A thought experiment in probability by Leonardo Barichello: two people are stranded on an island with only one banana to eat. To decide who gets it, they agree to play a game. Each of them will roll a fair 6-sided die. If the largest number rolled is a 1, 2, 3 or 4, then player 1 gets the banana. If the largest number rolled is a 5 or 6, then player 2 gets it. Which player has the better chance?
Perhaps somewhat surprising, but player 2 has the better chance of winning the game. The table below lists the 36 possible outcomes of two rolls with a 6-sided die. With a fair die, each of these 36 possible outcomes has an equal chance of being rolled. Of these, there are 16 possible outcomes where player 1 wins (44.4%, indicated in green) and 20 possible outcomes where player 2 wins (55.6%, indicated in blue).
| roll1 | roll2 | winner |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 1 |
| 1 | 4 | 1 |
| 1 | 5 | 2 |
| 1 | 6 | 2 |
| 2 | 1 | 1 |
| 2 | 2 | 1 |
| 2 | 3 | 1 |
| roll1 | roll2 | winner |
|---|---|---|
| 2 | 4 | 1 |
| 2 | 5 | 2 |
| 2 | 6 | 2 |
| 3 | 1 | 1 |
| 3 | 2 | 1 |
| 3 | 3 | 1 |
| 3 | 4 | 1 |
| 3 | 5 | 2 |
| 3 | 6 | 2 |
| roll1 | roll2 | winner |
|---|---|---|
| 4 | 1 | 1 |
| 4 | 2 | 1 |
| 4 | 3 | 1 |
| 4 | 4 | 1 |
| 4 | 5 | 2 |
| 4 | 6 | 2 |
| 5 | 1 | 2 |
| 5 | 2 | 2 |
| 5 | 3 | 2 |
| roll1 | roll2 | winner |
|---|---|---|
| 5 | 4 | 2 |
| 5 | 5 | 2 |
| 5 | 6 | 2 |
| 6 | 1 | 2 |
| 6 | 2 | 2 |
| 6 | 3 | 2 |
| 6 | 4 | 2 |
| 6 | 5 | 2 |
| 6 | 6 | 2 |
Assignment
In an extension to this thought experiment, both players roll a fair $$n$$-sided die ($$n \geq 4$$). The sides of the die are marked with 1 to $$n$$ eyes. The outcome of a roll with this die is represented as an integer (int) between 1 and $$n$$.

Player 1 wins the game if the roll of both players is less than or equal to an upper limit $$L \in \mathbb{N}$$ ($$1 \leq L \leq n$$) that has been fixed in advance. Otherwise, player 2 wins the game. Your task:
-
Write a function has_won that takes three arguments: i) the outcome (int) of a roll of the die by player 1, ii) the outcome (int) of a roll of the die by player 2 and iii) the upper limit $$L$$ (int). The function must return a Boolean value (bool) that indicates whether player 1 has won the game.
-
Write a function winning_outcomes that takes two arguments: i) the number of sides $$n$$ (int) of the die and ii) the upper limit $$L$$ (int). The function must return a tuple with two numbers (int): i) the number of possible outcomes from two rolls with an $$n$$-sided die where player 1 wins and ii) the number of possible outcomes from two rolls with an $$n$$-sided die where player 2 wins.
Tip
To determine the number of winning outcomes for both players, the function may go through all possible outcomes from two rolls with an $$n$$-sided die and determine who wins the game for each possible outcome.
-
Write a function odds that takes two arguments: i) the number of sides $$n$$ (int) of the fair die and ii) the upper limit $$L$$ (int). The function must return a tuple with two numbers (float): i) the probability of player 1 winning the game and ii) the probability of player 2 winning the game. Both probabilities must be expressed as a percentage.
Tip
The probability (as a percentage) of a player winning the game is equal to the number of possible outcomes where the player wins the game, divided by the total number of possible outcomes, times 100.
-
Write a function winner that takes two arguments: i) the number of sides $$n$$ (int) of the fair die and ii) the upper limit $$L$$ (int). The function must return an integer (int): the value 0 if both players have an equal chance of winning, the value 1 if player 1 has the better chance of winning, and the value 2 if player 2 has the better chance of winning.
Example
>>> has_won(3, 2, 4)
True
>>> has_won(1, 5, 4)
False
>>> winning_outcomes(6, 4)
(16, 20)
>>> odds(6, 4)
(44.44444444444444, 55.55555555555556)
>>> winner(6, 4)
2
Epilogue
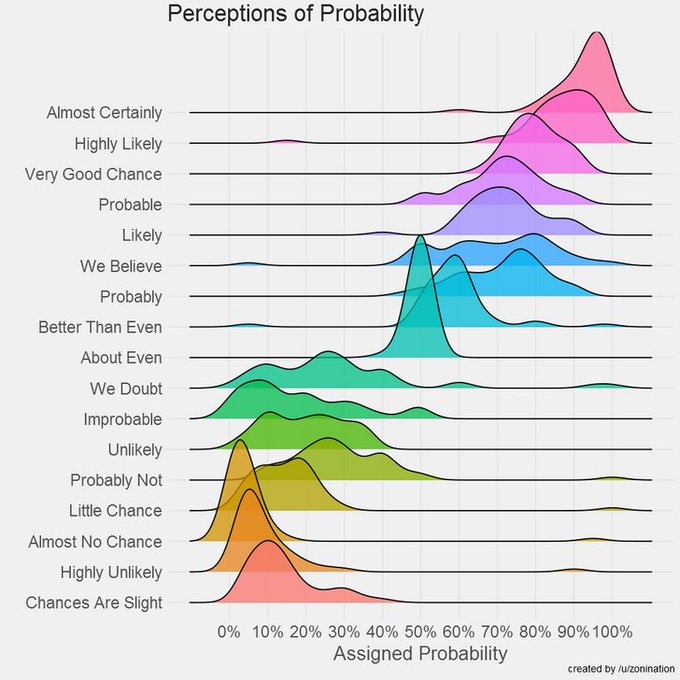
What kind of probability are people talking about when they say something has "almost no chance" or it's "almost certain"? This chart1 brilliantly explains visualizing the perceptions of probability.