The chef of a restaurant is quite sloppy. When he prepares a stack of pancakes, they come all out in different sizes. However, the maitre d'hotel mandates his waiters to rearrange the pancakes so that the smallest winds up on top, and so on, down to the largest at the bottom, before they deliver them to the guests at the tables.
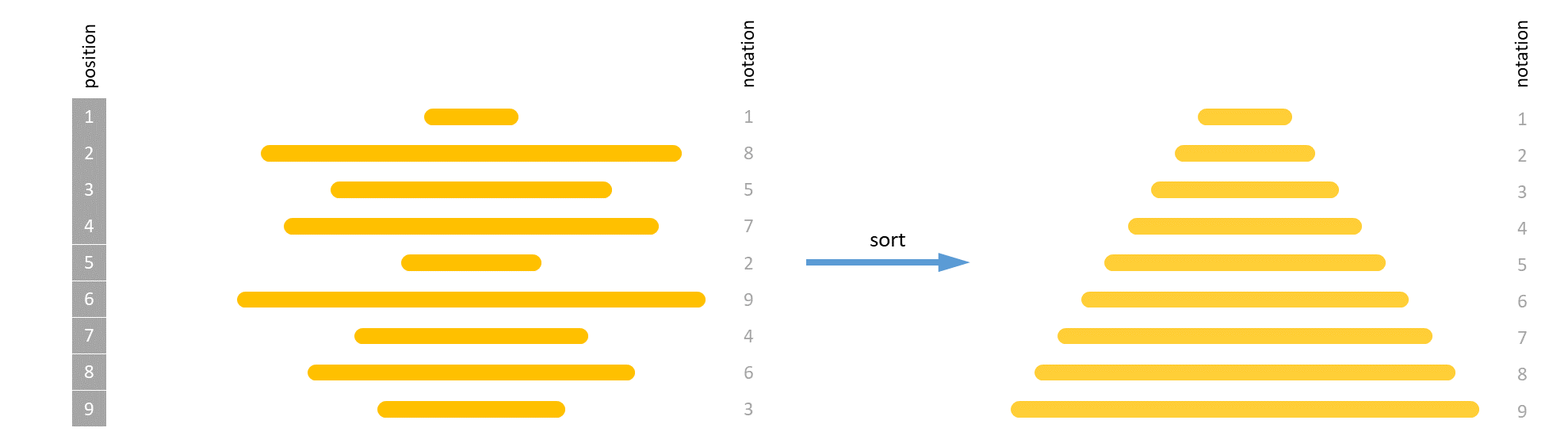
The waiters may perform only one operation to sort a stack of pancakes: a spatula can be inserted at any point in the stack and used to flip all pancakes above it. They may repeat this operation as many times as necessary, varying the number of pancakes flipped. To speed up their work, the waiters have turned pancake sorting into a sport of minimizing the number of flips.
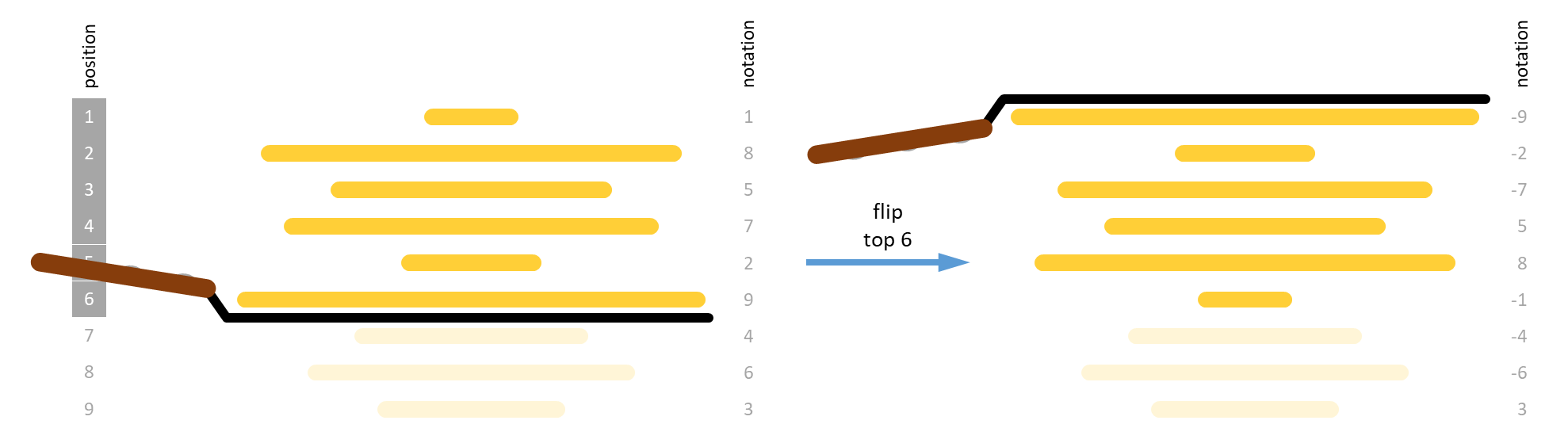
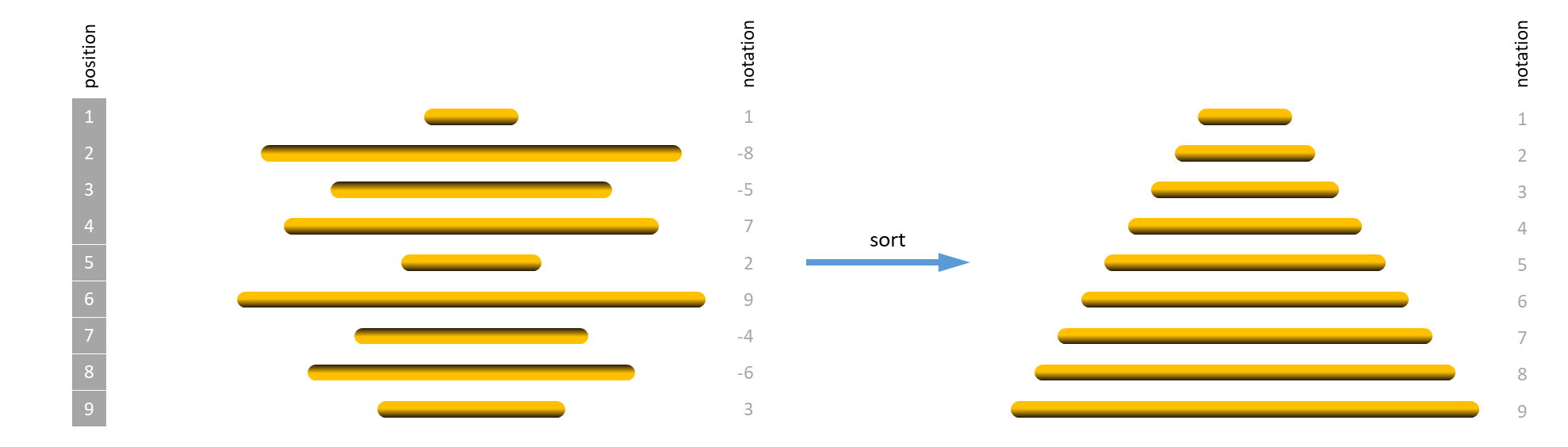
The challenge becomes even harder if the chef has been drinking too much, causing him to burn the bottom side of all pancakes. In that case, the maitre d'hotel does not only expect the waiters to sort the pancakes from the smallest to the largest, but also to ensure that all pancakes are flipped with their burnt side down.
Flipping a number of pancakes at the top of the stack does not only invert their order, but also reverses each individual pancake. As a result, a pancake having its burnt side up will have its burnt side down after flipping, and vice versa.
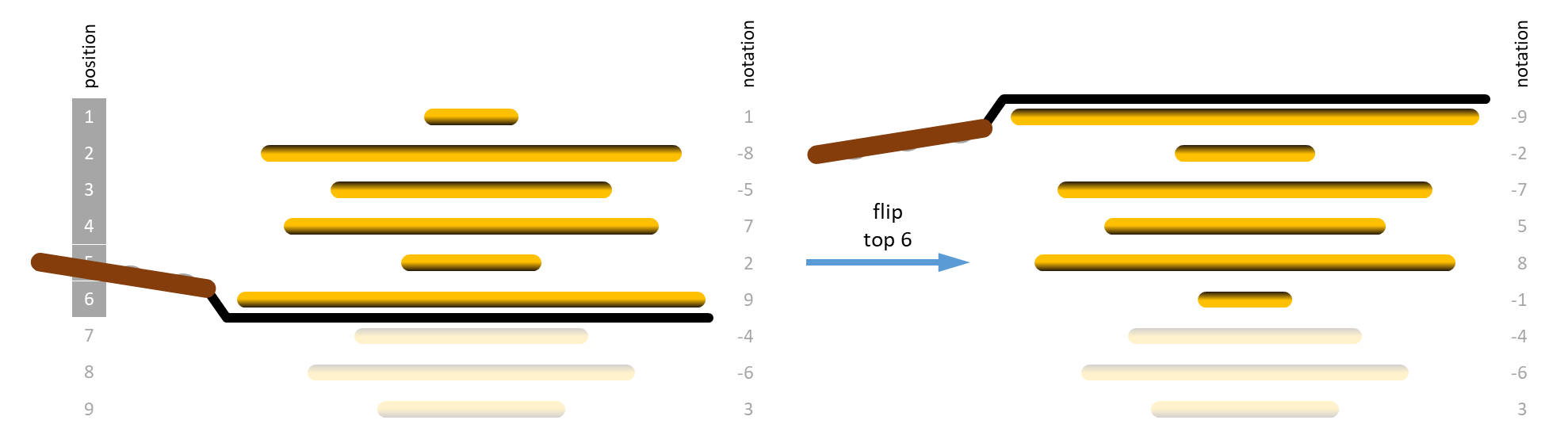
There is a simple algorithm for sorting a stack of $$n$$ pancakes. We explain it by numbering the positions of the pancakes top to bottom, starting from 1. Each sorting step of the algorithm assures that the largest among the top $$m$$ ($$1 \leq m \leq n$$) pancakes moves to position $$m$$, and has its burnt side down if the pancakes in the stack are burnt.
-
find the position $$i$$ ($$1 \leq i \leq m$$) of the largest pancake among the top $$m$$ pancakes
-
flip the top $$i$$ pancakes, so that the largest pancake winds up on top
-
only for burnt pancakes: flip the top pancake if it has its burnt side down, so that its burnt side comes up
-
flip the top $$m$$ pancakes, so that the largest pancake moves to position $$m$$ (and has its burnt side down if the pancakes in the stack are burnt)
To sort the entire stack of pancakes, all we need to do is repeat this sorting step for the top $$n$$ pancakes ($$m = n$$), the top $$n-1$$ pancakes ($$m = n-1$$), …, the top $$2$$ pancakes ($$m = 2$$) and the top pancake ($$m = 1$$).
Assignment
A pancake is represented by a number $$p \in \mathbb{Z}_0$$ (int). For an unroasted pancake we have $$p \in \mathbb{N}_0$$, with the value $$p$$ indicating the size of the pancake. For a burnt pancake the absolute value $$|p|$$ indicates the size of the pancake and the sign of $$p$$ indicates the position of the burnt side: down if $$p > 0$$ and up if $$p < 0$$.
A stack of $$n$$ pancakes is represented by a tuple (tuple) containing the representations of the $$n$$ pancakes in the stack, listed from top to bottom. A stack never has two pancakes with the same size. In other words, the representation of each pancake in a stack has a unique absolute value. A stack either has no burnt pancakes, or all pancakes in the stack are burnt on one side.
Your task is to sort a given stack of $$n \in \mathbb{N}_0$$ pancakes according to the simple algorithm outlined in the introduction. This is done by writing the following functions that each take a stack of $$n$$ pancakes as their first argument. Except for the function find_largest, all other functions have an optional parameter burnt that takes a Boolean value (default value: False). This parameter indicates whether the stack of pancakes is burnt (True) or not (False).
-
A function flip that returns the stack of pancakes obtained after flipping all pancakes in the given stack.
-
A function flip_top that has a second mandatory parameter that takes a number $$m$$ ($$1 \leq m \leq n$$, int). The function must return the stack of pancakes obtained after flipping the top $$m$$ pancakes in the given stack.
-
A function find_largest that has a second mandatory parameter that takes a number $$m$$ ($$1 \leq m \leq n$$, int). The function must return the position of the largest pancake among the top $$m$$ pancakes in the given stack.
-
A function sorting_step that has a second mandatory parameter that takes a number $$m$$ ($$1 \leq m \leq n$$, int). The function must return the stack of pancakes obtained after performing the sorting step for the top $$m$$ pancakes in the given stack.
-
A function sorting_steps that returns a list (list) containing stacks of pancakes. The given stack of pancakes is the first element in the list. The function must sort the given stack of pancakes by repeating the sorting step for the top $$n$$ pancakes, the top $$n-1$$ pancakes, …, the top $$2$$ pancakes and the top pancake. For each sorting step that changes the stack of pancakes, the stack of pancakes obtained after having performed the sorting step must be added to the end of the list.
Example
>>> flip((9, 2, 7, 5, 8, 1, 4, 6, 3))
(3, 6, 4, 1, 8, 5, 7, 2, 9)
>>> flip((-9, -2, -7, 5, 8, -1, -4, -6, 3), burnt=True)
(-3, 6, 4, 1, -8, -5, 7, 2, 9)
>>> flip_top((1, 4, 6, 3, 5, 2, 7, 8, 9), 3)
(6, 4, 1, 3, 5, 2, 7, 8, 9)
>>> flip_top((6, 4, 1, 3, 5, 2, 7, 8, 9), 6)
(2, 5, 3, 1, 4, 6, 7, 8, 9)
>>> flip_top((-1, -4, -6, 3, -5, -2, 7, 8, 9), 3, burnt=True)
(6, 4, 1, 3, -5, -2, 7, 8, 9)
>>> flip_top((6, 4, 1, 3, -5, -2, 7, 8, 9), 1, burnt=True)
(-6, 4, 1, 3, -5, -2, 7, 8, 9)
>>> flip_top((-6, 4, 1, 3, -5, -2, 7, 8, 9), 6, burnt=True)
(2, 5, -3, -1, -4, 6, 7, 8, 9)
>>> find_largest((1, 4, 6, 3, 5, 2, 7, 8, 9), 6)
3
>>> find_largest((-1, -4, -6, 3, -5, -2, 7, 8, 9), 6)
3
>>> sorting_step((1, 4, 6, 3, 5, 2, 7, 8, 9), 6)
(2, 5, 3, 1, 4, 6, 7, 8, 9)
>>> sorting_step((-1, -4, -6, 3, -5, -2, 7, 8, 9), 6, burnt=True)
(2, 5, -3, -1, -4, 6, 7, 8, 9)
>>> sorting_steps((1, 8, 5, 7, 2, 9, 4, 6, 3))
[(1, 8, 5, 7, 2, 9, 4, 6, 3), (3, 6, 4, 1, 8, 5, 7, 2, 9), (2, 7, 5, 3, 6, 4, 1, 8, 9), (1, 4, 6, 3, 5, 2, 7, 8, 9), (2, 5, 3, 1, 4, 6, 7, 8, 9), (4, 1, 3, 2, 5, 6, 7, 8, 9), (2, 3, 1, 4, 5, 6, 7, 8, 9), (1, 2, 3, 4, 5, 6, 7, 8, 9)]
>>> sorting_steps((1, -8, -5, 7, 2, 9, -4, -6, 3), burnt=True)
[(1, -8, -5, 7, 2, 9, -4, -6, 3), (-3, 6, 4, 1, -8, -5, 7, 2, 9), (-2, -7, 5, -3, 6, 4, 1, 8, 9), (-1, -4, -6, 3, -5, -2, 7, 8, 9), (2, 5, -3, -1, -4, 6, 7, 8, 9), (4, 1, 3, 2, 5, 6, 7, 8, 9), (-2, -3, -1, 4, 5, 6, 7, 8, 9), (1, -2, 3, 4, 5, 6, 7, 8, 9), (1, 2, 3, 4, 5, 6, 7, 8, 9)]
Epilogue
The simple algorithm used in this assignment does not minimize the number of flips needed to sort a stack of pancakes. However, it turns out to be quite a hard problem to find the minimal number of flips needed. The problem is notable as the topic of the only well-known mathematics paper by Microsoft founder Bill Gates (as William Gates), entitled Bounds for sorting by prefix reversal. Published in 1979, it describes an efficient algorithm for pancake sorting. In addition, the most notable paper published by Futurama co-creator David X. Cohen (as David S. Cohen) concerned the burnt pancake problem. Their collaborators were Christos Papadimitriou (then at Harvard, now at Columbia) and Manuel Blum (then at Berkeley, now at Carnegie Mellon University), respectively.
In 2008, a group of undergraduate students built a bacterial computer that can solve a simple example of the burnt pancake problem by programming E. coli to flip segments of DNA which are analogous to burnt pancakes. DNA has an orientation (5' and 3') and an order (promoter before coding). Even though the processing power expressed by DNA flips is low, the high number of bacteria in a culture provides a large parallel computing platform. The bacteria report when they have solved the problem by becoming antibiotic resistant.
Resources
-
Cohen DS, Blum M (1995). On the problem of sorting burnt pancakes. Discrete Applied Mathematics 61(2), 105–120.
-
Gates WH, Papadimitriou CH (1979). Bounds for sorting by prefix reversal. Discrete Mathematics 27(1), 47–57.
-
Haynes KA, Broderick ML, Brown AD, Butner TL, Dickson JO, Harden WL, Heard LH, Jessen EL, Malloy KJ, Ogden BJ, Rosemond S (2008). Engineering bacteria to solve the burnt pancake problem. Journal of Biological Engineering 2(1), 8.