De Parsons Code for Melodic Contours (of kortweg Parsons code) is een eenvoudige manier om muziekfragmenten te identificeren door middel van melodische beweging - de beweging van de toonhoogte naar boven en naar beneden. Denys Parsons ontwikkelde het systeem voor zijn boek The Directory of Tunes and Musical Themes uit 1975. In de Parsons code wordt de eerste noot van een melodie voorgesteld door een asterisk (*). Elke volgende noot wordt genoteerd aan de hand van één van drie mogelijke letters die de relatie van de toonhoogte van de noot aangeven in vergelijking met de voorgaande noot:

• de letter U (up) als de noot hoger is dan de vorige noot
• de letter D (down) als de noot lager is dan de vorige noot
• de letter R (repeat) als de noot dezelfde toonhoogte heeft als de vorige noot

Deze letters worden de bewegingen van de melodie genoemd. Het verschil in toonhoogte tussen twee opeenvolgende noten wordt in deze voorstelling dus genegeerd. Hieronder zie je bijvoorbeeld een grafische voorstelling van de Parsons code voor het refrein van Love Me Tender van Elvis Presley.

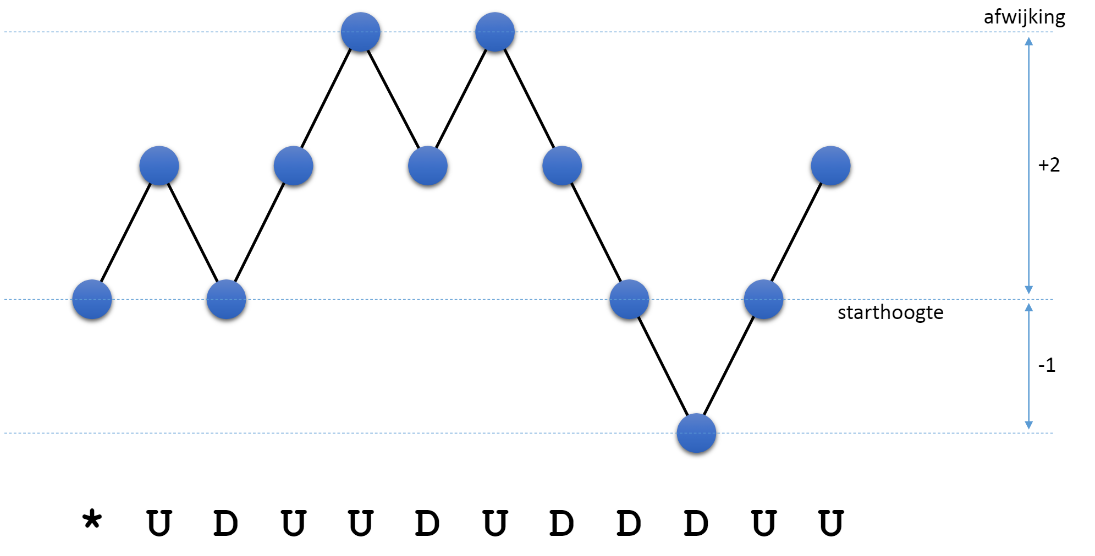
Een reeks van drie opeenvolgende bewegingen wordt een triplet genoemd. Een reeks van vier opeenvolgende bewegingen wordt een quadruplet genoemd. Het maximaal aantal stappen dat een Parsons code afwijkt van de starthoogte wordt de maximale afwijking van de code genoemd. Zo heeft het bovenstaande voorbeeld een maximale afwijking van 2 (maximaal twee stappen boven de starthoogte en maximaal één stap onder de starthoogte).

Opgave

Elke regel van het tekstbestand parsons.txt¹ bevat de Parsons code van een melodie, gevolgd door één enkele spatie en een woord dat zelf geen spaties bevat. Gevraagd wordt:

1. Bepaal reguliere expressies voor elk van onderstaande verzamelingen. Daarbij staat $$\mathcal{P}$$ voor de verzameling van alle mogelijke Parsons codes. Probeer de reguliere expressies bovendien zo kort mogelijk te houden.

   • $$\alpha = \{ p \in \mathcal{P}\,|\,$$ eerste en laatste triplet van $$p$$ zijn elkaars spiegelbeeld $$\}$$

     voorbeelden:	*UDRUUUUDRURDDRDU $$\in \alpha$$
     	*DUURUDDUUDDRRDD $$\not\in \alpha$$

   • $$\beta = \{ p \in \mathcal{P}\,|\,$$ $$p$$ bevat een quadruplet dat minstens drie keer (niet overlappend) voorkomt $$\}$$

     voorbeelden:	*DDRUURUUDUURUDUUURURD $$\in \beta$$
     	*RRDDDDUDDRRRURDDDUDDRU $$\not\in \beta$$

   • $$\gamma = \{ p \in \mathcal{P}\,|\,$$ elk triplet van $$p$$ bevat twee voorkomens van eenzelfde beweging $$\}$$

     voorbeelden:	*UDDRDRRDRDDRDDUUURRDD $$\in \gamma$$
     	*URRUURDRURUURURUDDR $$\not\in \gamma$$

   • $$\delta = \{ p \in \mathcal{P}\,|\,$$ $$p$$ heeft een maximale afwijking van ten hoogste 1 $$\}$$

     voorbeelden:	*DRRUUDDRUURDUDURDDU $$\in \delta$$ (maximale afwijking 1)
     	*UDUUDUDDDUU $$\not\in \delta$$ (melodie Love Me Tender: maximale afwijking 2)

   Gebruik een commando uit de grep familie om enkel die regels van het bestand parsons.txt² te selecteren, waarvan de reeks letters van de Parsons code behoort tot de opgegeven verzameling.

2. Beschouw de verzamelingen $$\alpha$$, $$\beta$$, $$\gamma$$ en $$\delta$$ zoals hierboven gedefinieerd. Gebruik nu deze verzamelingen om op de volgende manier een boodschap bestaande uit vier woorden te achterhalen:

   • Het eerste woord staat op unieke regel met het patroon uit de verzameling $$\alpha \cap \beta$$

   • Het tweede woord staat op unieke regel met het patroon uit de verzameling $$\beta \cap \gamma$$

   • Het derde woord staat op unieke regel met het patroon uit de verzameling $$\gamma \cap \delta$$

   • Het vierde woord staat op unieke regel met het patroon uit de verzameling $$\delta \cap \alpha$$

   Geef telkens een Unix commando dat elk van deze woorden opzoekt in het bestand en uitschrijft naar standaard uitvoer (zonder het patroon dat aan het woord voorafgaat). Hierbij is het dus niet toegelaten om het woord letterlijk uit te schrijven (bv. echo xxx).