A protein is a long chain of amino acids. The protein chain is not straight, but it is folded in a way that minimizes the potential energy. Our goal is to calculate how the protein will fold itself. In this assignment we will therefore consider a simple model of protein folding in which amino acids are either hydrophobic or hydrophilic. Hydrophobic amino acids tend to clump together.

For simplicity, we will represent proteins as binary strings in which ones correspond to hydrophobic amino acids and zeros correspond to hydrophilic amino acids. The string (protein) should then be folded into a two-dimensional square grid. The goal is to make the hydrophobic amino acids stick together, i.e. to get as many ones as possible to be close to each other. Hence, we have an optimization problem where the objective function is the number of pairs of ones that are next to each other in the grid (horizontally or vertically) without being next to each other in the string.

You should design an algorithm using dynamic programming to construct an optimal accordion fold of a given protein string of length $$n$$. An accordion fold is a fold where the first string goes straight down, then goes straight up, then goes straight down, and so on. In such a fold, it can be observed that the vertical pairs of adjacent ones will always result in the string, so it's only horizontal pairs of ones that contribute to the objective function.

The figure below shows the string 00110001001100001001000001 that is accordion folded in such a way that the objective function is 4.

Accordion fold of protein 00110001001100001001000001 that has score 4.

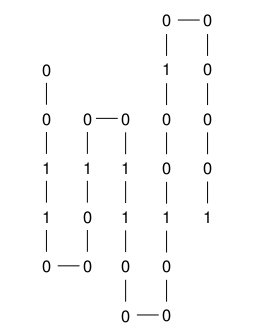
Assignment

In this assignment we will work with strings containing zeros and ones only, representing proteins containing hydrophobic (zeros) and hydrophilic (ones) amino acids. An accordion folding of such a protein is represented as a list of strings containing zeros and ones only, with the list elements representing the individual traits of the accordion folding. The score of a protein folded string is computed as the number of pairs of ones located next to each other in the folded protein, but that are not consecutive in the string itself. Your task:

Write a function foldingScore that takes a protein containing hydrophobic and hydrophilic amino acids. The function must return the maximal score that can be obtained by accordion folding the given protein.
Write a function optimalFolding that takes a protein containing hydrophobic and hydrophilic amino acids. The function must return an optimal accordion folding of the given protein (i.e. an accordion folding resulting in the maximal score). If multiple optimal accordion foldings exist, the function may return any of these solutions.

Example

        >>> foldingScore('00110001001100001001000001')
4

>>> optimalFolding('00110001001100001001000001')
['00', '11000', '10011000010', '01000001']