If we take a front view look at a row of apartments standing next to each other, we see that their number of floors varies. We can therefore describe the row of apartments as a sequence (list or tuple) of natural numbers (int) that indicate the number of floors in each apartment (listed from left to right). This way, the sequence $$[1, 4, 3, 2, 3, 1]$$ represents the following row of apartments.
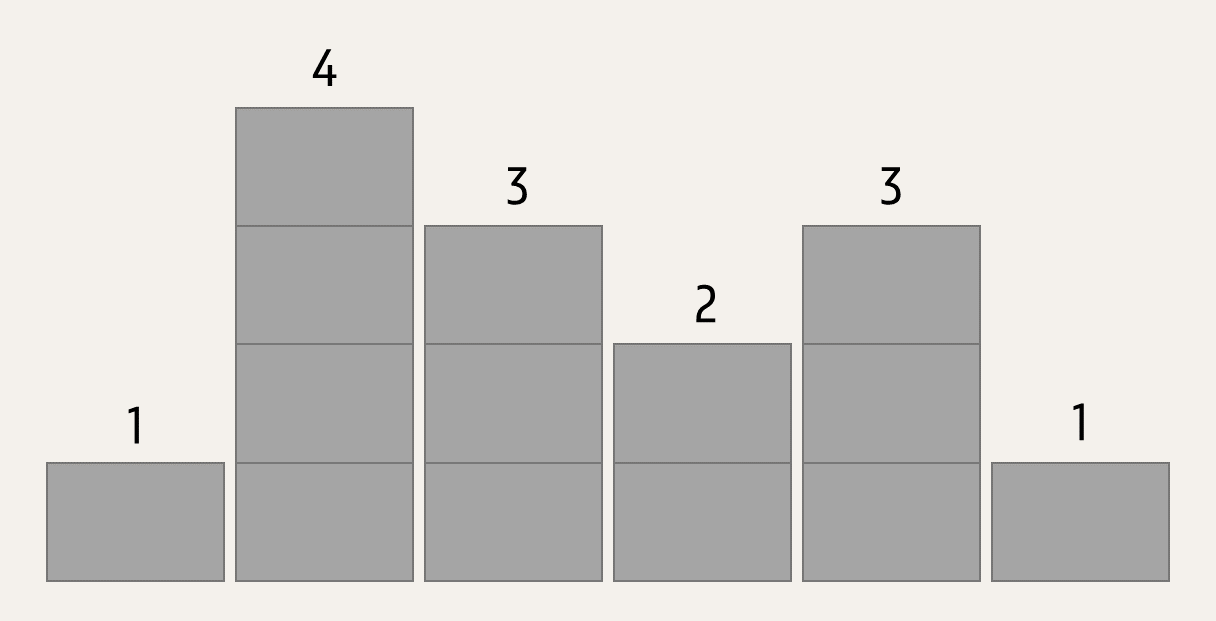
Those apartments look quite boring, so we decide to make them more colorful. On each floor, we paint as many apartments as possible in the same color using a single horizontal brush stroke. We always change color when we change floors or when there's a gap between two apartments on a given floor.
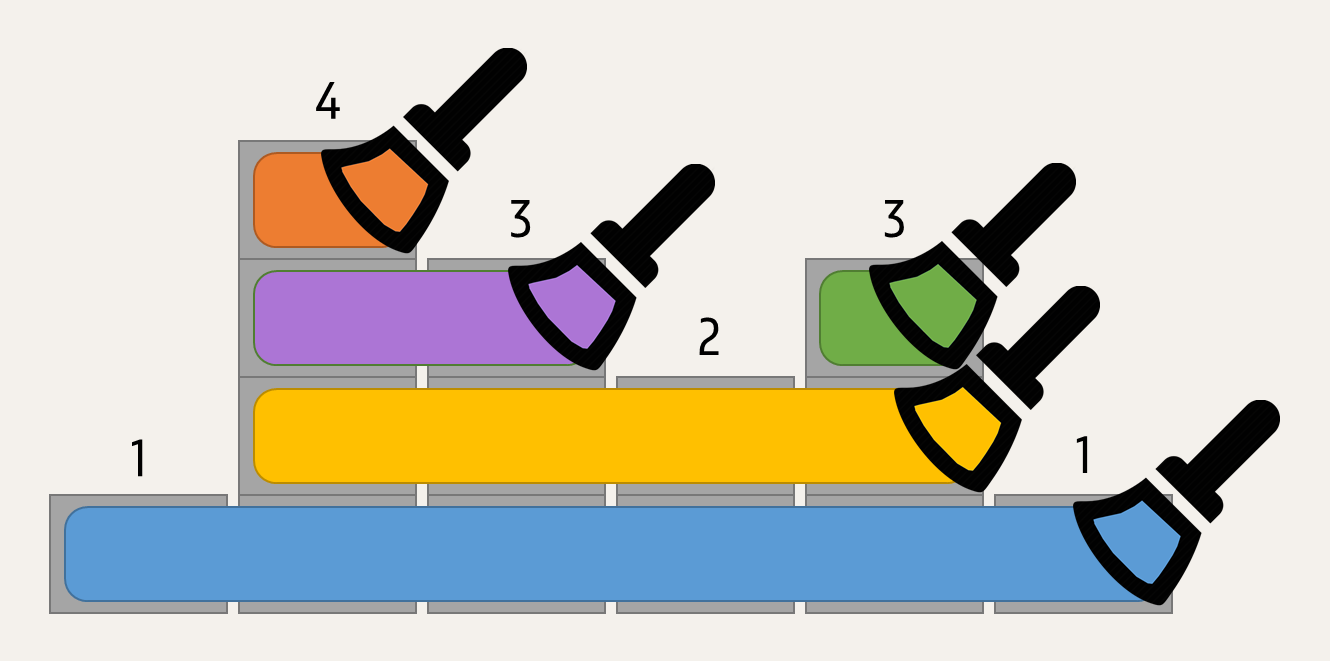
If we color the apartments $$[1, 4, 3, 2, 3, 1]$$ bottom up, we start painting the first floor of all six apartments in blue with a first stroke. With a second stroke we paint the second floor of four apartments in yellow. The third stroke covers the third floor of two apartments in purple and a fourth stroke paints the third floor of one more apartment in green. Finally, we need a fifth stroke to give the fourth floor of one apartment an orange color. So in total we need five brush strokes to paint all apartments in five different colors.
Assignment
A row of apartments is represented as a sequence (list or tuple) of natural numbers (int) that indicate the number of floors in each apartment (listed from left to right). Your task:
-
Write a function floors that takes a row of $$n$$ apartments. The function must return a list of $$m$$ floors (listed from top to bottom), where $$m$$ equals the number of floors in the tallest apartment. Each floor is itself represented as a list of $$n$$ Boolean values (bool) that indicate if the apartment at the corresponding position reaches to the given floor.
-
Write a function front_view that returns a representation (str) of the front view look at a row of apartments. The number of lines in the representation must equal the number of floors in the tallest apartment. The format of the representation can be derived from the example below. The row of $$n$$ apartments must be passed as an argument to the function. In addition, the function also has the following optional parameters:
-
width (int; default value: 3): width of the representation of one apartment, expressed as a number of characters
-
distance (int; default value: 1): distance between the representations of two apartments, expressed as a number of characters
-
apartment (str; default value: #): a single character that is used to represent apartments
-
air (str; default value: space): a single character that is used to represent air (where there are no apartments)
-
-
Write a function brush_strokes that takes a row of $$n$$ apartments. The function must return the number of brush strokes needed (and also the number of different colors used) to paint the given row of apartments according to the procedure outlined above.
Example
>>> apartments = (1, 4, 3, 2, 3, 1)
>>> floors(apartments)
[[False, True, False, False, False, False], [False, True, True, False, True, False], [False, True, True, True, True, False], [True, True, True, True, True, True]]
>>> print(front_view(apartments, air='~'))
~~~~###~~~~~~~~~~~~~~~~
~~~~###~###~~~~~###~~~~
~~~~###~###~###~###~~~~
###~###~###~###~###~###
>>> print(front_view(apartments, width=4, distance=0, apartment='<', air="-"))
----<<<<----------------
----<<<<<<<<----<<<<----
----<<<<<<<<<<<<<<<<----
<<<<<<<<<<<<<<<<<<<<<<<<
>>> brush_strokes(apartments)
5