The number \(\pi\) can be approximated in the following way. Consider a square measuring 1 by 1. If you throw a dart into that square in a random location, the probability that it will have a distance of 1 or less to the lower left corner is \(\pi/4\).

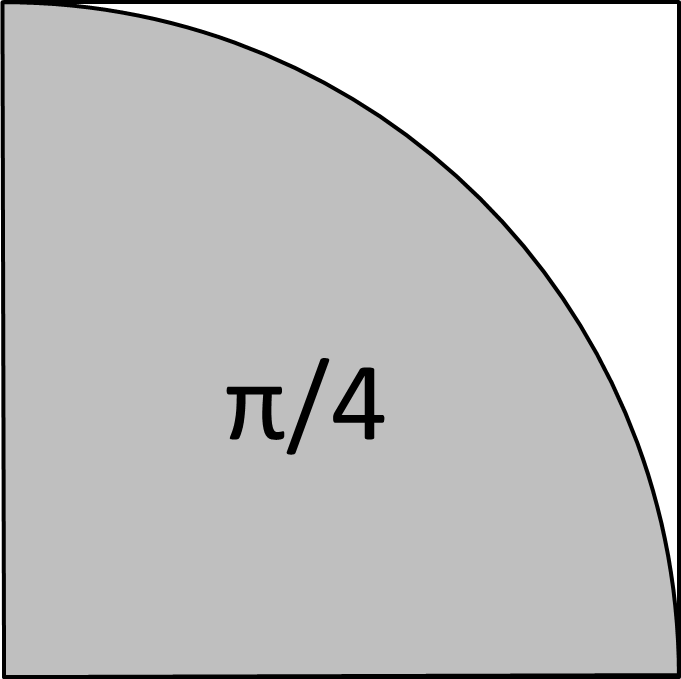
To see why that is, remember that the area of a circle with a radius of 1 is \(\pi\), so the area of a quarter circle is \(\pi/4\). Thus, if a dart lands in a random point in the square, the chance that it lands in the quarter circle with its centre at the lower left corner is \(\pi/4\). Therefore, if you throw \(n\) darts into the square, and \(m\) of those land inside a distance of 1 to the lower left corner, then \(4M/N\) approximates \(\pi\) if \(n\) is very large.

Input

An integer \(n \in \mathbb{N}_0\).

Output

Simulate throwing \(n\) darts on a square measuring 1 by 1. Determine the number of darts that is within distance 1 to the lower left corner of the unit square. Print the value \(4m/n\).

Tip

Use the random() function from the random module.

Tip

The distance of a point \((x, y)\) to the lower-left corner is calculated as \(\sqrt{x^2 + y^2}\). .

Example

Input:

100000

Output:

3.13992