A Harshad or Niven number is a number $$h \in \mathbb{N}_0$$ that is divisible by the sum of its digits. Harshad numbers were defined by the Indian mathematician K.R. Kaprekar. The term Harshad stems from the Sanskrit harsa (joy) + da (give), and means "he who gives joy". The term Niven number refers to a presentation that was given by Ivan M. Niven about this type of numbers at a conference in 1977.
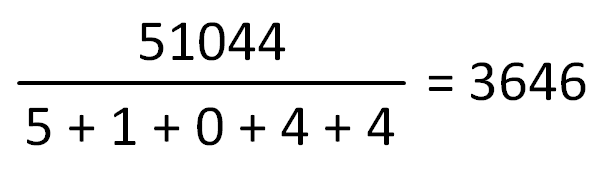
The first Harshad numbers larger than nine are (see sequence A0053491 in the OEIS)
10, 12, 18, 20, 21, 24, 27, 30, 36, 40, 42, 45, 48, 50, 54, 60, 63, 70, 72, 80, 81, 84, 90, 100, 102, 108, 110, 111, 112, 114, 117, 120, 126, 132, 133, 135, 140, 144, 150, 152, 153, 156, 162, 171, 180, 190, 192, 195, 198, 200, 201, 204, …
All numbers of one digit are by definition Harshad numbers.
Input
A number $$h \in \mathbb{N}_0$$.
Output
One line of text indicating whether or not the number $$h$$ is a Harshad number. The textual description must be of the same format as the examples below.
Example
Input:
153Output:
153 is a Harshad numberExample
Input:
1234Output:
1234 is not a Harshad numberResources
Kennedy RE, Cooper CN (1985). On the natural density of the Niven numbers. Abstracts of the American Mathematical Society 6, 17. 2
Sloane NJA, Plouffe S (1995). The encyclopedia of integer sequences. Academic Press. 3
Wells D (1986). The Penguin dictionary of curious and interesting numbers. Penguin Books, NY, 171. 4