New Jersey (United States) magician Karl Fulves¹ invented this extrasensory perception trick. Hand a friend an ordinary die and turn your back. Ask her to place the die on a table. Now ask her to give the die a quarter turn. If the top number is even, she must turn it to the east (to her right), and if the top number is odd, she must turn it north (away from her). This exposes a new top number, and she can turn the die again according to the same rule, turning it east if the number is even and north if it's odd.

After she has continued in this way for several turns, you ask her to stop when the top number is 1, then to give the die one final turn and to concentrate on the top number. It would seem as though the final number might be any one of four possibilities, but you can name it correctly with your back turned. How?

Explanation — after at most three moves, the die enters a recurring loop: 1 4 5 6 3 2. So after the first few turns, it's safe to predict that 4 will follow 1. Because the whole cycle is predictable, the trick can be repeated a few times to produce various "final" numbers.

Assignment

Define a class Die that can be used to represent dice that have been put in a certain way on a table in front of you. It must be possible to turn these dice in a given direction, according to the model described in the figure below. According to this model, dice are represented schematically such that each side of a die is made visible. For example, the central scheme represents a die with side 6 on top, side 3 to the back, side 4 to the front, side 2 to the left, side 5 to the right and side 1 at the bottom. The other four schemes indicate the position of the die after it has been turned from the central position to the north (top), to the south (bottom), to the east (right) or to the west (left).

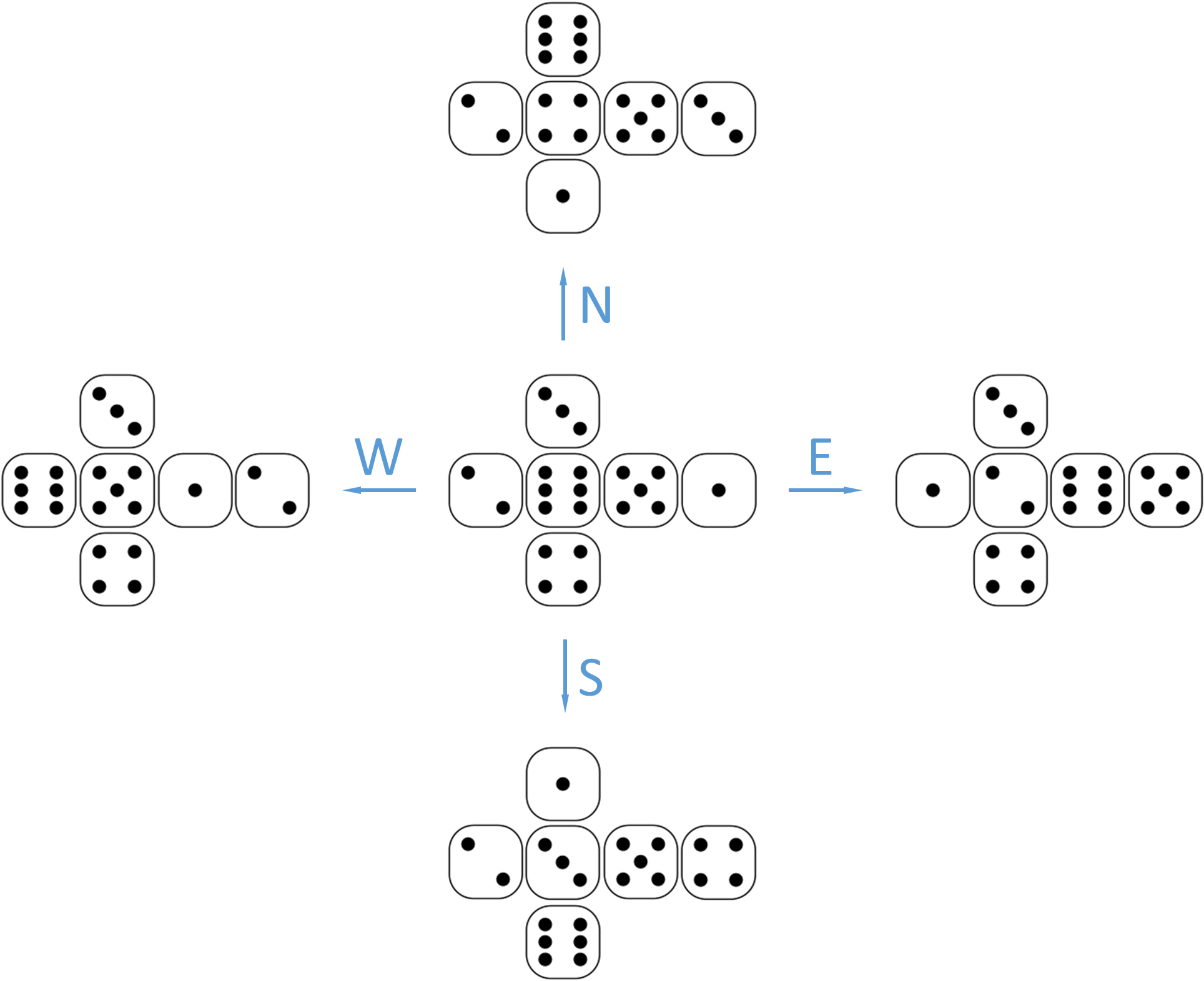
The class Die must support at least the following methods:

• An initialisation method that takes no arguments. Upon initialisation, a die is positioned as the central die in the above figure.

• A method topNumber that returns the number of pips on the top side of the die.

• A method __str__ that returns a string representation of the die that corresponds to the schematic representation used in the above figure. Take a look at the example session below to derive how this string representation must be formatted. Note that none of the lines in this string representation ends with white space characters.

• A method turn that takes an uppercase letter indicating which direction the die has to be turned: N for north, S for south, E for east and W for west. The method must not only make sure the die is turned in the given direction, but must also return the number of pips on the side that comes on top  after the die has been turned. In case an invalid direction is passed to the method, the die should not be turned and an AssertionError must be raised with the message invalid direction.

• A method sequence that takes a target value (an integer in the interval $[1,6]$). The method must return a list containing all numbers that come on top if the die is turned according to the method invented by Karl Fulves. Make sure the procedure is repeated at least three times until the target value is observed on top of the die, after which the procedure is repeated one more time. In execting the procedure, the die must also be turned in the given direction on each repetition of the procedure.

Example

                
            >>> die = Die()
>>> print(die)
  3
2 6 5 1
  4
>>> die.topNumber()
6
>>> die.turn('E')
2
>>> print(die)
  3
1 2 6 5
  4
>>> die.turn('W')
6
>>> print(die)
  3
2 6 5 1
  4
>>> die.turn('N')
4
>>> print(die)
  6
2 4 5 3
  1
>>> die.turn('S')
6
>>> print(die)
  3
2 6 5 1
  4
>>> die.turn('X')
Traceback (most recent call last):
AssertionError: invalid direction
>>> die.sequence(1)
[2, 1, 4, 5, 6, 3, 2, 1, 4]
>>> print(die)
  1
5 4 2 3
  6
>>> die.sequence(3)
[5, 6, 3, 2]
>>> print(die)
  3
1 2 6 5
  4