The Inca and a couple of other South American cultures from the Andean region used quipus (also known as khipus or talking knots): recording devices consisting of knotted strings. The word khipu — meaning "knot" or "to knot" — comes from the Cusco-Colloa Quechua language (Peru). A quipu usually consisted of colored, spun, and plied thread or strings made from cotton or camelid fiber. For the Inca, the system aided in collecting data and keeping records, ranging from monitoring tax obligations, properly collecting census records, calendrical information, and military organization. Only a relatively small number have survived. A quipu could have only a few or up to 2,000 cords.

Quipus certainly have not yet revealed all of their secrets, but it is clear now that most recorded information consists of numbers in a decimal system. Marcia and Robert Ascher — after having analyzed several hundred quipus — succeeded in deciphering the code that allows to read the numbers.
One cord can record one or more numbers. These numbers are represented as a sequence of knot clusters to be read from the main cord: the cord to which all the other cords are attached (at the top of the figure below). Each cluster of knots is a digit, and there are three main types of knots: simple overhand knots, figure-of-eight knots and long knots (consisting of an overhand knot with one or more additional turns).
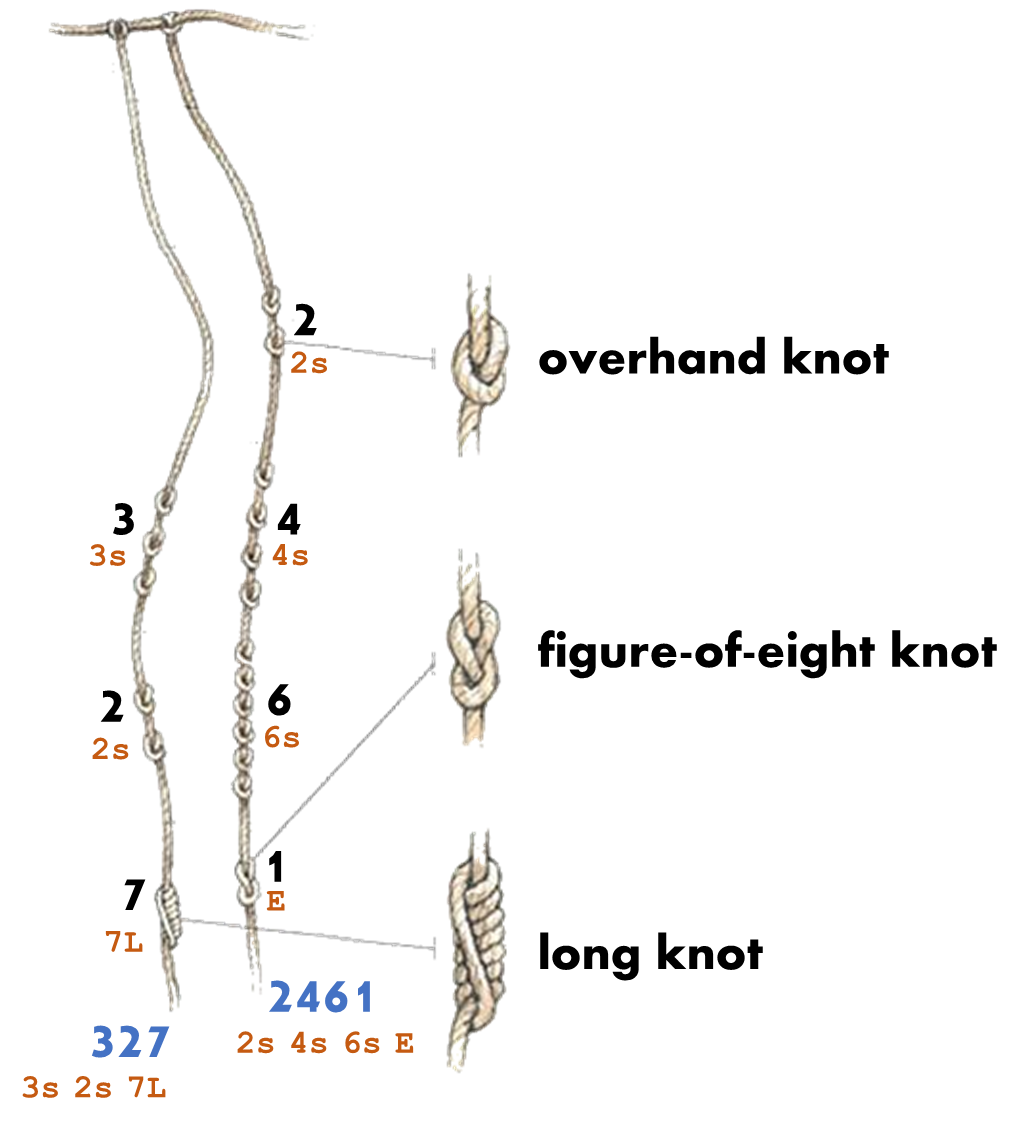
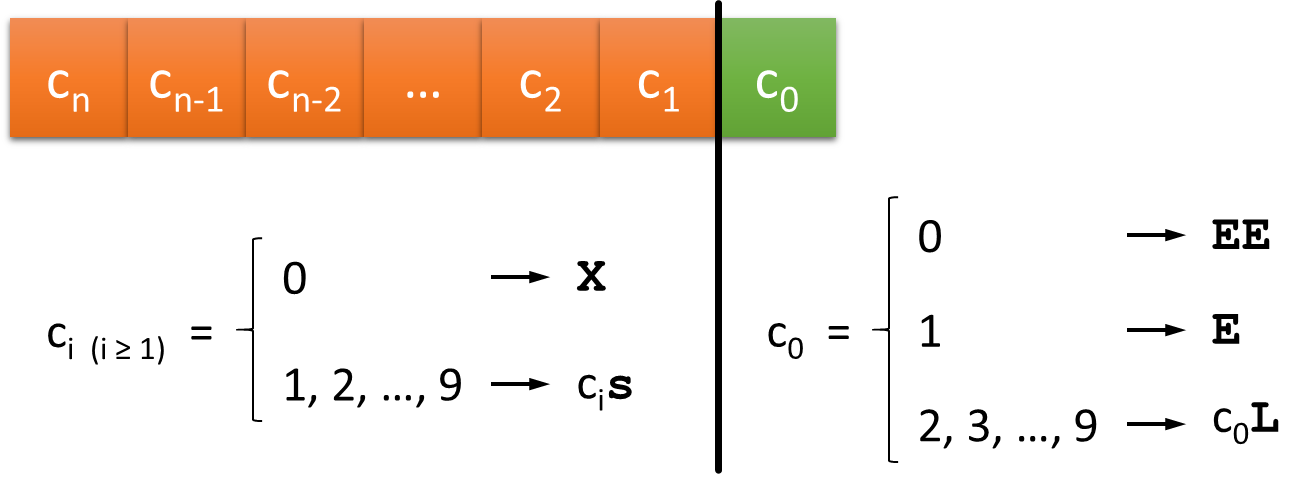
For their analysis of quipus the Aschers introduced a simple notation for a cluster of knots (known as the Aschers' notation). They discovered that a natural number $$c_{n}c_{n - 1}c_{n - 2}\ldots c_{2}c_{1}c_{0}$$ — with $$c_i (i = 0, 1, \ldots, n)$$ the digits $$0, 1, \ldots, 9$$ in the decimal representation of the number — is recorded in the following way using knots. For all digits except the last one, a zero is represented by the absence of a knot in the appropriate position (represented as X) and all other digits are represented by a cluster of $$c_i$$ overhand knots (represented as $$c_i$$s). For the last digit a zero is represented by a figure-of-eight knot with an extra twist (represented as EE), a one by a figure-of-eight knot (represented as E; a long knot with a single turn is the same as an overhand knot and would not discriminate the last digit) and the other digits by a long knot with $$c_i$$ turns (represented as $$c_i$$L). The representations of the individual clusters of knots are separated by spaces in the Aschers' notation.
Because the ones digit (the last digit of a natural number) is represented in a distinctive way, it is clear where each number ends. One strand on a quipu can therefore contain several numbers. This is summarized in the diagram below.
For example, if 3s represents three overhand knots, 7L represents a long knot with seven turns, E represents a figure-of-eight knot and X represents a space:
-
the number 327 is represented by 3s 2s 7L
-
the number 2461 is represented by 2s 4s 6s E
-
the number 107 followed by the number 51 is represented by 1s X 7L 5s E
This reading can be confirmed by a fortunate fact: quipus regularly contain sums in a systematic way. For instance, a cord may contain the sum of the next $$n$$ cords, and this relationship is repeated throughout the quipu. Sometimes there are sums of sums as well. Such a relationship would be very improbable if the knots were read incorrectly.
Assignment
Define the following functions that can be used to convert the decimal representation of a number $$n \in \mathbb{N}$$ (int) into the knots representation of $$n$$ on a quipu in the Aschers' notation (str), and vice versa.
-
Write a function decimal2ascher that takes a decimal number $$n \in \mathbb{N}$$ (int). If the argument passed to the function is not a positive integer, an AssertionError must be raised with the message invalid quipu. Otherwise the knots representation of $$n$$ on a quipu must be returned in the Aschers' notation (str).
-
Write a function ascher2decimal that takes the knot representation of a positive integer on a quipu in the Aschers' notation (str). If the argument passed to the function is not a string containing a valid knots representation in Aschers' notation of a number on a quipu, an AssertionError must be raised with the message invalid quipu. Otherwise the decimal representation of the number (int) must be returned.
Now also define a class Quipu that can be used to compute with quipus in Python. New objects of this class must either be initialized with the decimal representation of a number $$n \in \mathbb{N}$$ (int) or with the knots representation of $$n$$ on a quipu in the Aschers' notation (str). Other values passed upon initialization should result in an AssertionError being raised with the message invalid quipu.
The conversion of a quipu (an object of the class Quipu) into a string — using the built-in functions str() and repr() — always contains the knots representation on a quipu in the Aschers' notation (use the example below to derive the difference in formatting of the results returned by both built-in functions) and the conversion to an integer — using the built-in function int() — returns the decimal value.
Make sure that the binary operators for addition (+), subtraction (-), multiplication (*), integer division (//), modulo (%) and exponentiation (**) each evaluate to a new quipu (an object of the class Quipu) if both of their operands are quipus or if one operand is a quipu and the other is an integer. The result of these operations should have the same decimal value as the result obtained by applying these operators on two integer operands having the same decimal values. If the operations do not evaluate to a valid quipu, an AssertionError must be raised with the message invalid quipu.
Example
>>> decimal2ascher(327)
'3s 2s 7L'
>>> decimal2ascher(2461)
'2s 4s 6s E'
>>> decimal2ascher(107)
'1s X 7L'
>>> decimal2ascher(-1)
Traceback (most recent call last):
AssertionError: invalid quipu
>>> ascher2decimal('3s 2s 7L')
327
>>> ascher2decimal('2s 4s 6s E')
2461
>>> ascher2decimal('1s X 7L')
107
>>> ascher2decimal('5s 17s 4L')
Traceback (most recent call last):
AssertionError: invalid quipu
>>> number = Quipu('3s 2s 7L')
>>> int(number)
327
>>> str(number)
'3s 2s 7L'
>>> number
Quipu('3s 2s 7L')
>>> number = Quipu(2461)
>>> int(number)
2461
>>> str(number)
'2s 4s 6s E'
>>> number
Quipu('2s 4s 6s E')
>>> Quipu(42) + Quipu(16)
Quipu('5s 8L')
>>> Quipu(42) - Quipu(16)
Quipu('2s 6L')
>>> Quipu(42) * Quipu(16)
Quipu('6s 7s 2L')
>>> Quipu(42) // Quipu(16)
Quipu('2L')
>>> Quipu(42) % Quipu(16)
Quipu('1s EE')
>>> Quipu(12) ** Quipu(2)
Quipu('1s 4s 4L')
>>> Quipu(42) + 16
Quipu('5s 8L')
>>> Quipu(42) - 16
Quipu('2s 6L')
>>> Quipu(42) * 16
Quipu('6s 7s 2L')
>>> Quipu(42) // 16
Quipu('2L')
>>> Quipu(42) % 16
Quipu('1s EE')
>>> Quipu(12) ** 2
Quipu('1s 4s 4L')
>>> 42 + Quipu(16)
Quipu('5s 8L')
>>> 42 - Quipu(16)
Quipu('2s 6L')
>>> 42 * Quipu(16)
Quipu('6s 7s 2L')
>>> 42 // Quipu(16)
Quipu('2L')
>>> 42 % Quipu(16)
Quipu('1s EE')
>>> 12 ** Quipu(2)
Quipu('1s 4s 4L')
>>> Quipu('5s 17s 4L')
Traceback (most recent call last):
AssertionError: invalid quipu
>>> Quipu(-1)
Traceback (most recent call last):
AssertionError: invalid quipu
>>> Quipu({1, 2, 3})
Traceback (most recent call last):
AssertionError: invalid quipu
>>> Quipu(16) - Quipu(42)
Traceback (most recent call last):
AssertionError: invalid quipu